表达式编译

在我生命旅程的半途，我发现自己身处一片黑暗的森林，迷失了正路。

但丁·阿利吉耶里，《神曲·地狱篇》

本章令人兴奋，因为不止一个，不止两个，而是三个原因。首先，它提供了我们虚拟机执行管道中的最后一部分。一旦到位，我们就可以将用户的源代码从扫描一直连接到执行。

其次，我们将编写一个真正的、货真价实的编译器。它解析源代码并输出一系列低级的二进制指令。当然，它是字节码，而不是某个芯片的原生指令集，但它比 jlox 更接近底层。我们即将成为真正的语言黑客。

第三，最后，我想向你展示我最喜欢的算法之一：沃恩·普拉特的“自顶向下运算符优先级解析”。在我看来，它是解析表达式的最优雅方式。它优雅地处理前缀运算符、后缀运算符、中缀运算符、mixfix运算符，以及任何你想要的-fix运算符。它轻松地处理优先级和结合性。我喜欢它。

像往常一样，在我们开始有趣的部分之前，我们还需要处理一些准备工作。你必须先吃蔬菜，才能吃甜点。首先，让我们放弃我们为测试扫描器而编写的临时脚手架，并用更实用的东西替换它。

InterpretResult interpret(const char* source) {

  Chunk chunk;
  initChunk(&chunk);

  if (!compile(source, &chunk)) {
    freeChunk(&chunk);
    return INTERPRET_COMPILE_ERROR;
  }

  vm.chunk = &chunk;
  vm.ip = vm.chunk->code;

  InterpretResult result = run();

  freeChunk(&chunk);
  return result;

}

我们创建一个新的空块并将其传递给编译器。编译器将获取用户的程序并用字节码填充块。至少，如果程序没有编译错误，它会这样做。如果遇到错误，compile() 返回 false，我们丢弃不可用的块。

否则，我们将完成的块发送给虚拟机执行。虚拟机完成后，我们释放块，就完成了。如你所见，compile() 的签名现在不同了。

#define clox_compiler_h

#include "vm.h"

bool compile(const char* source, Chunk* chunk);

#endif

我们将编译器将写入代码的块传递进去，然后 compile() 返回编译是否成功。我们在实现中对签名进行了同样的更改。

#include "scanner.h"

bool compile(const char* source, Chunk* chunk) {

  initScanner(source);

对 initScanner() 的调用是本章中唯一幸存的代码。删除我们为测试扫描器而编写的临时代码，并用以下三行代码替换它

  initScanner(source);

  advance();
  expression();
  consume(TOKEN_EOF, "Expect end of expression.");

}

对 advance() 的调用“启动”了扫描器。我们很快就会看到它做了什么。然后我们解析单个表达式。我们还没有要处理语句，所以这是我们支持的语法的唯一子集。当我们在几章之后添加语句时，我们将重新讨论这一点。解析表达式后，我们应该到达源代码的末尾，因此我们检查是否有哨兵 EOF 标记。

我们将花费本章的剩余时间来使此函数正常工作，特别是那个小小的 expression() 调用。通常，我们会直接深入到该函数定义，并从上到下逐步完成实现。

本章不同。普拉特的解析技术一旦你掌握了所有内容，就会变得非常简单，但将其分解成小块有点棘手。它当然是递归的，这是问题的一部分。但它也依赖于一个大型数据表。当我们构建算法时，该表会增加额外的列。

我不想每次扩展表时都重新讨论 40 多行代码。因此，我们将从解析器的外部逐步进入核心，并在进入核心之前介绍所有周围的部分。这将比大多数章节需要更多的耐心和心理空间，但这是我能做到的最好的方法。

17 . 1单趟编译

编译器大致有两个任务。它解析用户的源代码以了解其含义。然后它利用这些知识并输出产生相同语义的低级指令。许多语言将这两个角色在实现中分为两个独立的阶段。解析器生成 AST—就像 jlox 所做的那样—，然后代码生成器遍历 AST 并输出目标代码。

在 clox 中，我们采用了一种老式的做法，将这两个阶段合并为一个。在过去，语言黑客这样做是因为计算机根本没有足够的内存来存储整个源文件的 AST。我们这样做是因为它使我们的编译器更简单，这在用 C 语言编程时是一个真正的优势。

像我们要构建的单趟编译器并不适合所有语言。由于编译器在生成代码时只能窥视用户的程序，因此语言的设计必须使得在理解语法时不需要太多周围的上下文。幸运的是，小型动态类型的 Lox 非常适合这种情况。

在实际应用中，这意味着我们的“编译器” C 模块具有你在 jlox 中熟悉的解析功能—消费标记、匹配预期标记类型等。它还具有用于代码生成的功能—发出字节码并将常量添加到目标块。（这也意味着我将在本章以及以后的章节中交替使用“解析”和“编译”。）

我们先构建解析和代码生成部分。然后，我们将它们与中间的代码缝合在一起，这些代码使用普拉特的方法解析 Lox 的特定语法并输出正确的字节码。

17 . 2解析标记

首先，是编译器的前半部分。这个函数的名字应该很熟悉。

#include "scanner.h"

static void advance() {
  parser.previous = parser.current;

  for (;;) {
    parser.current = scanToken();
    if (parser.current.type != TOKEN_ERROR) break;

    errorAtCurrent(parser.current.start);
  }
}

就像在 jlox 中一样，它在标记流中向前移动。它向扫描器请求下一个标记并将其存储以备后用。在此之前，它会获取旧的 current 标记，并将其存储在 previous 字段中。这将对我们稍后很有用，这样我们就可以在匹配标记后获取词素。

读取下一个标记的代码包含在一个循环中。请记住，clox 的扫描器不报告词法错误。相反，它创建特殊的错误标记，并将报告它们的责任留给解析器。我们在这里这样做。

我们不断循环，读取标记并报告错误，直到遇到一个非错误标记或到达末尾。这样一来，解析器的其余部分只会看到有效的标记。当前标记和先前标记存储在这个结构中

#include "scanner.h"

typedef struct {
  Token current;
  Token previous;
} Parser;

Parser parser;

static void advance() {

就像我们在其他模块中所做的那样，我们有一个此结构类型的全局变量，这样我们就不需要在编译器中的函数之间传递状态。

17 . 2 . 1处理语法错误

如果扫描器给我们一个错误标记，我们需要真正告诉用户。这是使用以下方法实现的

static void errorAtCurrent(const char* message) {
  errorAt(&parser.current, message);
}

我们从当前标记中提取位置，以便告诉用户错误发生的位置，并将其转发给 errorAt()。更常见的是，我们将报告我们刚刚消耗的标记位置的错误，因此我们将更短的名称赋予此函数

static void error(const char* message) {
  errorAt(&parser.previous, message);
}

实际的工作发生在这里

static void errorAt(Token* token, const char* message) {
  fprintf(stderr, "[line %d] Error", token->line);

  if (token->type == TOKEN_EOF) {
    fprintf(stderr, " at end");
  } else if (token->type == TOKEN_ERROR) {
    // Nothing.
  } else {
    fprintf(stderr, " at '%.*s'", token->length, token->start);
  }

  fprintf(stderr, ": %s\n", message);
  parser.hadError = true;
}

首先，我们打印错误发生的位置。如果词素是人类可读的，我们尝试显示它。然后我们打印错误消息本身。之后，我们设置 hadError 标志。这记录了在编译过程中是否发生了任何错误。此字段也位于解析器结构中。

  Token previous;

  bool hadError;

} Parser;

之前我说过，如果发生错误，compile() 应该返回 false。现在我们可以让它这样做。

  consume(TOKEN_EOF, "Expect end of expression.");

  return !parser.hadError;

}

我还有另一个标志要介绍用于错误处理。我们希望避免错误级联。如果用户在代码中犯了一个错误，并且解析器对它在语法中的位置感到困惑，我们不希望它在第一个错误之后喷出一堆毫无意义的连锁错误。

我们在 jlox 中使用恐慌模式错误恢复来解决这个问题。在 Java 解释器中，我们抛出一个异常，以从所有解析器代码中解开，直到我们可以跳过标记并重新同步。我们在 C 中没有异常。相反，我们将进行一些障眼法。我们添加一个标志来跟踪我们当前是否处于恐慌模式。

  bool hadError;

  bool panicMode;

} Parser;

当发生错误时，我们设置它。

static void errorAt(Token* token, const char* message) {

  parser.panicMode = true;

  fprintf(stderr, "[line %d] Error", token->line);

之后，我们继续像往常一样编译，就好像错误从未发生过一样。字节码永远不会被执行，因此继续前进是无害的。诀窍在于，当恐慌模式标志被设置时，我们只是抑制检测到的任何其他错误。

static void errorAt(Token* token, const char* message) {

  if (parser.panicMode) return;

  parser.panicMode = true;

解析器很有可能偏离轨道，但用户不会知道，因为所有错误都被吞掉了。当解析器到达同步点时，恐慌模式结束。对于 Lox，我们选择了语句边界，因此当我们稍后将它们添加到编译器中时，我们将清除该标志。

这些新字段需要初始化。

  initScanner(source);

  parser.hadError = false;
  parser.panicMode = false;

  advance();

为了显示错误，我们需要一个标准标头。

#include <stdio.h>

#include <stdlib.h>

#include "common.h"

还有一个最后的解析函数，这是我们从 jlox 中熟悉的另一个老朋友。

static void consume(TokenType type, const char* message) {
  if (parser.current.type == type) {
    advance();
    return;
  }

  errorAtCurrent(message);
}

它与 advance() 类似，因为它读取下一个标记。但它还会验证标记是否具有预期的类型。如果不是，它会报告错误。此函数是编译器中大多数语法错误的基础。

好的，目前为止前端的内容就到这里了。

17 . 3发射字节码

在解析并理解用户程序的一部分之后，下一步是将其翻译成一系列字节码指令。它从最简单的步骤开始：将单个字节附加到块中。

static void emitByte(uint8_t byte) {
  writeChunk(currentChunk(), byte, parser.previous.line);
}

很难相信伟大的事情会通过这样一个简单的函数流淌。它写入给定的字节，该字节可能是指令的操作码或操作数。它会发送上一个标记的行信息，以便运行时错误与该行相关联。

我们正在写入的块被传递到 compile() 中，但它需要传送到 emitByte()。为此，我们依赖于此中间函数

Parser parser;

Chunk* compilingChunk;

static Chunk* currentChunk() {
  return compilingChunk;
}

static void errorAt(Token* token, const char* message) {

现在，块指针存储在模块级变量中，就像我们存储其他全局状态一样。稍后，当我们开始编译用户定义的函数时，“当前块”的概念会变得更加复杂。为了避免不得不回去更改大量代码，我把这些逻辑封装在 currentChunk() 函数中。

我们在写入任何字节码之前初始化这个新的模块变量

bool compile(const char* source, Chunk* chunk) {
  initScanner(source);

  compilingChunk = chunk;

  parser.hadError = false;

然后，在最后，当我们完成块的编译时，我们将事情总结起来。

  consume(TOKEN_EOF, "Expect end of expression.");

  endCompiler();

  return !parser.hadError;

它调用了这个

static void endCompiler() {
  emitReturn();
}

在本节中，我们的 VM 仅处理表达式。当您运行 clox 时，它将解析、编译并执行单个表达式，然后打印结果。为了打印该值，我们暂时使用 OP_RETURN 指令。因此，我们让编译器在块末尾添加一个这样的指令。

static void emitReturn() {
  emitByte(OP_RETURN);
}

既然我们已经来到后端，我们不妨让自己生活得更轻松一些。

static void emitBytes(uint8_t byte1, uint8_t byte2) {
  emitByte(byte1);
  emitByte(byte2);
}

随着时间的推移，我们会遇到很多需要编写一个操作码和一个字节操作数的情况，因此定义这个方便函数是值得的。

17 . 4解析前缀表达式

我们已经组装了我们的解析和代码生成实用函数。缺少的部分是连接这些的中间代码。

compile() 中我们唯一需要实现的步骤是这个函数

static void expression() {
  // What goes here?
}

我们还没有准备好实现 Lox 中所有类型的表达式。事实上，我们甚至还没有布尔值。在本节中，我们只关心以下四种情况

• 数字字面量：123
• 用于分组的圆括号：(123)
• 一元否定：-123
• 算术运算的四种方式：+、-、*、/

当我们完成编译这些表达式类型的函数时，我们也会组装调用它们的表驱动解析器的要求。

17 . 4 . 1标记的解析器

现在，让我们关注 Lox 表达式，这些表达式每个都只有一个标记。在本节中，这只包含数字字面量，但稍后还会有更多。以下是如何编译它们

我们将每个标记类型映射到不同的表达式类型。我们为每个表达式定义一个函数，该函数输出相应的字节码。然后我们构建一个函数指针数组。数组中的索引对应于 TokenType 枚举值，每个索引处的函数是编译该标记类型表达式的代码。

为了编译数字字面量，我们将指向以下函数的指针存储在数组的 TOKEN_NUMBER 索引处。

static void number() {
  double value = strtod(parser.previous.start, NULL);
  emitConstant(value);
}

我们假设数字字面量的标记已经消耗掉了，并且存储在 previous 中。我们获取该字面量，并使用 C 标准库将其转换为双精度值。然后，我们使用此函数生成加载该值的代码

static void emitConstant(Value value) {
  emitBytes(OP_CONSTANT, makeConstant(value));
}

首先，我们将该值添加到常量表中，然后我们发出一个 OP_CONSTANT 指令，该指令在运行时将该值压入堆栈。为了在常量表中插入一个条目，我们依赖于

static uint8_t makeConstant(Value value) {
  int constant = addConstant(currentChunk(), value);
  if (constant > UINT8_MAX) {
    error("Too many constants in one chunk.");
    return 0;
  }

  return (uint8_t)constant;
}

大部分工作都在 addConstant() 中完成，我们在前面的章节中定义了它。它将给定的值添加到块的常量表末尾，并返回其索引。新函数的工作主要是确保我们没有过多的常量。由于 OP_CONSTANT 指令使用单个字节作为索引操作数，因此我们只能在块中存储和加载最多256个常量。

基本上就是这样。只要有一些合适的代码可以消耗 TOKEN_NUMBER 标记，在函数指针数组中查找 number()，然后调用它，我们就可以将数字字面量编译成字节码。

17 . 4 . 2用于分组的圆括号

如果每个表达式都只有一行标记，那么我们假设的解析函数指针数组会很棒。可惜，大多数表达式要长一些。但是，许多表达式以特定标记开始。我们称这些为前缀表达式。例如，当我们解析一个表达式并且当前标记是 ( 时，我们知道我们一定是在查看一个带括号的分组表达式。

事实证明，我们的函数指针数组也处理这些。表达式类型的解析函数可以消耗任何它想要的额外标记，就像在普通的递归下降解析器中一样。以下是括号的工作原理

static void grouping() {
  expression();
  consume(TOKEN_RIGHT_PAREN, "Expect ')' after expression.");
}

同样，我们假设初始的 ( 已经消耗掉了。我们递归地调用 expression() 来编译括号之间的表达式，然后解析最后的 )。

就后端而言，分组表达式实际上什么都没有。它的唯一功能是语法的—它允许您在需要更高优先级的表达式中插入一个更低优先级的表达式。因此，它本身没有任何运行时语义，因此不会发出任何字节码。对 expression() 的内部调用负责为括号内的表达式生成字节码。

17 . 4 . 3一元否定

一元减号也是一个前缀表达式，因此它也适用于我们的模型。

static void unary() {
  TokenType operatorType = parser.previous.type;

  // Compile the operand.
  expression();

  // Emit the operator instruction.
  switch (operatorType) {
    case TOKEN_MINUS: emitByte(OP_NEGATE); break;
    default: return; // Unreachable.
  }
}

前面的 - 标记已经消耗掉了，并且位于 parser.previous 中。我们从其中获取标记类型以记录我们正在处理的一元运算符。现在还不需要这样做，但在我们使用这个函数来编译下一章中的 ! 运算符时，这将更有意义。

就像在 grouping() 中一样，我们递归地调用 expression() 来编译操作数。之后，我们发出执行否定的字节码。将否定指令放在操作数的字节码之后看起来可能有点奇怪，因为 - 出现在左侧，但从执行顺序的角度考虑一下

1. 我们首先评估操作数，这会将其值留在堆栈上。

2. 然后我们弹出该值，对其取反，并将结果压入堆栈。

因此，OP_NEGATE 指令应该最后发出。这是编译器的工作的一部分—按源代码中出现的顺序解析程序，并将其重新排列成执行发生的顺序。

但是，这段代码有一个问题。它调用的 expression() 函数将解析操作数的任何表达式，无论优先级如何。一旦我们添加二元运算符和其他语法，它就会做错事。考虑

-a.b + c;

在这里，- 的操作数应该只是 a.b 表达式，而不是整个 a.b + c。但是，如果 unary() 调用 expression()，后者将愉快地处理所有剩余的代码，包括 +。它会错误地将 - 视为比 + 优先级低。

当解析一元 - 的操作数时，我们需要只编译特定优先级或更高优先级的表达式。在 jlox 的递归下降解析器中，我们通过调用要允许的最低优先级表达式的解析方法（在本例中为 call()）来实现这一点。解析特定表达式的每个方法也解析了任何更高优先级的表达式，因此这也包括优先级表中的其他部分。

clox 中的 number() 和 unary() 之类的解析函数有所不同。它们每个只解析一种类型的表达式。它们不会级联以包含更高优先级的表达式类型。我们需要一个不同的解决方案，看起来像这样

static void parsePrecedence(Precedence precedence) {
  // What goes here?
}

这个函数—一旦我们实现它—从当前标记开始，解析给定优先级或更高优先级的任何表达式。我们还有一些其他设置需要完成，然后才能编写这个函数的主体，但您可能已经猜到它会使用我一直在讨论的解析函数指针表。现在，不要太担心它是如何工作的。为了将“优先级”作为参数，我们用数字定义它。

} Parser;

typedef enum {
  PREC_NONE,
  PREC_ASSIGNMENT,  // =
  PREC_OR,          // or
  PREC_AND,         // and
  PREC_EQUALITY,    // == !=
  PREC_COMPARISON,  // < > <= >=
  PREC_TERM,        // + -
  PREC_FACTOR,      // * /
  PREC_UNARY,       // ! -
  PREC_CALL,        // . ()
  PREC_PRIMARY
} Precedence;

Parser parser;

这些都是 Lox 中的优先级级别，从最低到最高排列。由于 C 为枚举隐式地分配了连续更大的数字，这意味着 PREC_CALL 在数字上大于 PREC_UNARY。例如，假设编译器位于一段代码上，例如

-a.b + c

如果我们调用 parsePrecedence(PREC_ASSIGNMENT)，那么它将解析整个表达式，因为 + 的优先级高于赋值。如果我们改为调用 parsePrecedence(PREC_UNARY)，它将编译 -a.b 并停止。它不会继续执行 +，因为加法的优先级低于一元运算符。

有了这个函数，我们可以轻松地填写 expression() 的缺失主体。

static void expression() {

  parsePrecedence(PREC_ASSIGNMENT);

}

我们只需解析最低优先级级别，它也包含所有更高优先级的表达式。现在，为了编译一元表达式的操作数，我们调用这个新函数，并将其限制在相应的级别

  // Compile the operand.

  parsePrecedence(PREC_UNARY);

  // Emit the operator instruction.

我们使用一元运算符自身的 PREC_UNARY 优先级来允许嵌套的一元表达式，比如 !!doubleNegative。由于一元运算符的优先级很高，因此它会正确地排除诸如二元运算符之类的操作。说到二元运算符 . . . 

17 . 5解析中缀表达式

二元运算符不同于前面的表达式，因为它们是中缀的。对于其他表达式，我们从第一个标记就能知道我们正在解析什么。对于中缀表达式，我们只有在解析完它的左操作数后，并在中间偶然发现运算符标记时，才能知道我们正在解析二元运算符。

这里有一个例子

1 + 2

让我们一起看看如何用我们目前掌握的知识来编译它。

1. 我们调用 `expression()`。它反过来调用 `parsePrecedence(PREC_ASSIGNMENT)`。

2. 该函数（一旦我们实现它）会看到前面的数字标记，并识别出它正在解析一个数字字面量。它将控制权移交给 `number()`。

3. `number()` 创建一个常量，发出一个 `OP_CONSTANT`，然后返回到 `parsePrecedence()`。

现在怎么办？对 `parsePrecedence()` 的调用应该消耗整个加法表达式，所以它需要以某种方式继续。幸运的是，解析器恰好处于我们需要的状态。现在我们已经编译了前面的数字表达式，下一个标记是 `+`。这正是 `parsePrecedence()` 需要检测到的标记，表明我们处于一个中缀表达式的中间，并且需要意识到我们已经编译的表达式实际上是该表达式的操作数。

所以这个假设的函数指针数组并不仅仅列出解析以给定标记开头的表达式的函数。相反，它是一个表格，包含函数指针。第一列将前缀解析函数与标记类型关联起来。第二列将中缀解析函数与标记类型关联起来。

我们将用作 `TOKEN_PLUS`、`TOKEN_MINUS`、`TOKEN_STAR` 和 `TOKEN_SLASH` 的中缀解析器的函数是：

static void binary() {
  TokenType operatorType = parser.previous.type;
  ParseRule* rule = getRule(operatorType);
  parsePrecedence((Precedence)(rule->precedence + 1));

  switch (operatorType) {
    case TOKEN_PLUS:          emitByte(OP_ADD); break;
    case TOKEN_MINUS:         emitByte(OP_SUBTRACT); break;
    case TOKEN_STAR:          emitByte(OP_MULTIPLY); break;
    case TOKEN_SLASH:         emitByte(OP_DIVIDE); break;
    default: return; // Unreachable.
  }
}

当调用前缀解析函数时，前面的标记已经被消耗了。中缀解析函数则更深入—整个左操作数表达式已经编译完成，并且随后的中缀运算符也被消耗掉了。

左操作数首先被编译的事实运作良好。这意味着在运行时，该代码会首先执行。当它运行时，它产生的值最终会出现在堆栈上。这正是中缀运算符需要它的地方。

然后我们来到 `binary()` 来处理其余的算术运算符。该函数编译右操作数，就像 `unary()` 编译它自己的尾随操作数一样。最后，它发出执行二元运算的字节码指令。

在运行时，VM 会按顺序执行左操作数和右操作数代码，将它们的值留在堆栈上。然后它执行运算符的指令。它弹出这两个值，计算运算结果，并将结果压入堆栈。

这里可能吸引你注意的代码是 `getRule()` 那行。当解析右手操作数时，我们再次需要担心优先级。以这样的表达式为例：

2 * 3 + 4

当解析 `*` 表达式的右操作数时，我们需要捕获的是 `3`，而不是 `3 + 4`，因为 `+` 的优先级低于 `*`。我们可以为每个二元运算符定义一个单独的函数。每个函数都会调用 `parsePrecedence()` 并传入其操作数的正确优先级级别。

但这有点繁琐。每个二元运算符的右操作数优先级比它本身高一级higher。我们可以使用这个 `getRule()` 方法（我们很快就会讲到）动态地查找它。利用它，我们用比该运算符级别高一级别的优先级调用 `parsePrecedence()`。

这样，即使所有二元运算符的优先级不同，我们也可以使用单个 `binary()` 函数来处理它们。

17 . 6普拉特解析器

我们现在已经把编译器的所有零部件都列出来了。我们有针对每个语法产生式的函数：`number()`、`grouping()`、`unary()` 和 `binary()`。我们还需要实现 `parsePrecedence()` 和 `getRule()`。我们还知道，我们需要一个表格，它可以根据标记类型，找到

• 用于编译以该类型标记开头的前缀表达式的函数，

• 用于编译其左操作数后跟该类型标记的中缀表达式的函数，以及

• 使用该标记作为运算符的infix表达式的优先级。

我们将这三个属性封装在一个小结构体中，它代表解析表格中的一行。

} Precedence;

typedef struct {
  ParseFn prefix;
  ParseFn infix;
  Precedence precedence;
} ParseRule;

Parser parser;

该 ParseFn 类型是针对不带参数且不返回值的函数类型的一个简单的typedef。

} Precedence;

typedef void (*ParseFn)();

typedef struct {

驱动整个解析器的表格是一个 ParseRules 数组。我们一直在讨论它，终于可以看到了。

ParseRule rules[] = {
  [TOKEN_LEFT_PAREN]    = {grouping, NULL,   PREC_NONE},
  [TOKEN_RIGHT_PAREN]   = {NULL,     NULL,   PREC_NONE},
  [TOKEN_LEFT_BRACE]    = {NULL,     NULL,   PREC_NONE}, 
  [TOKEN_RIGHT_BRACE]   = {NULL,     NULL,   PREC_NONE},
  [TOKEN_COMMA]         = {NULL,     NULL,   PREC_NONE},
  [TOKEN_DOT]           = {NULL,     NULL,   PREC_NONE},
  [TOKEN_MINUS]         = {unary,    binary, PREC_TERM},
  [TOKEN_PLUS]          = {NULL,     binary, PREC_TERM},
  [TOKEN_SEMICOLON]     = {NULL,     NULL,   PREC_NONE},
  [TOKEN_SLASH]         = {NULL,     binary, PREC_FACTOR},
  [TOKEN_STAR]          = {NULL,     binary, PREC_FACTOR},
  [TOKEN_BANG]          = {NULL,     NULL,   PREC_NONE},
  [TOKEN_BANG_EQUAL]    = {NULL,     NULL,   PREC_NONE},
  [TOKEN_EQUAL]         = {NULL,     NULL,   PREC_NONE},
  [TOKEN_EQUAL_EQUAL]   = {NULL,     NULL,   PREC_NONE},
  [TOKEN_GREATER]       = {NULL,     NULL,   PREC_NONE},
  [TOKEN_GREATER_EQUAL] = {NULL,     NULL,   PREC_NONE},
  [TOKEN_LESS]          = {NULL,     NULL,   PREC_NONE},
  [TOKEN_LESS_EQUAL]    = {NULL,     NULL,   PREC_NONE},
  [TOKEN_IDENTIFIER]    = {NULL,     NULL,   PREC_NONE},
  [TOKEN_STRING]        = {NULL,     NULL,   PREC_NONE},
  [TOKEN_NUMBER]        = {number,   NULL,   PREC_NONE},
  [TOKEN_AND]           = {NULL,     NULL,   PREC_NONE},
  [TOKEN_CLASS]         = {NULL,     NULL,   PREC_NONE},
  [TOKEN_ELSE]          = {NULL,     NULL,   PREC_NONE},
  [TOKEN_FALSE]         = {NULL,     NULL,   PREC_NONE},
  [TOKEN_FOR]           = {NULL,     NULL,   PREC_NONE},
  [TOKEN_FUN]           = {NULL,     NULL,   PREC_NONE},
  [TOKEN_IF]            = {NULL,     NULL,   PREC_NONE},
  [TOKEN_NIL]           = {NULL,     NULL,   PREC_NONE},
  [TOKEN_OR]            = {NULL,     NULL,   PREC_NONE},
  [TOKEN_PRINT]         = {NULL,     NULL,   PREC_NONE},
  [TOKEN_RETURN]        = {NULL,     NULL,   PREC_NONE},
  [TOKEN_SUPER]         = {NULL,     NULL,   PREC_NONE},
  [TOKEN_THIS]          = {NULL,     NULL,   PREC_NONE},
  [TOKEN_TRUE]          = {NULL,     NULL,   PREC_NONE},
  [TOKEN_VAR]           = {NULL,     NULL,   PREC_NONE},
  [TOKEN_WHILE]         = {NULL,     NULL,   PREC_NONE},
  [TOKEN_ERROR]         = {NULL,     NULL,   PREC_NONE},
  [TOKEN_EOF]           = {NULL,     NULL,   PREC_NONE},
};

你可以看到 `grouping` 和 `unary` 如何分别插到它们各自的标记类型的列中，作为前缀解析器。在下一列中，`binary` 连接到四个算术中缀运算符。这些中缀运算符的优先级也在最后一列中设置。

除了这些之外，表格的其余部分都充满了 `NULL` 和 `PREC_NONE`。这些空单元格中，大多数是因为这些标记没有与之关联的表达式。例如，你不能以 `else` 开头一个表达式，而 `}` 会是一个非常令人困惑的中缀运算符。

但是，我们还没有填完整个语法。在后面的章节中，随着我们添加新的表达式类型，这些插槽中会有一些函数。我喜欢这种解析方法的一点是，它可以很容易地看到哪些标记被语法使用，哪些标记是可用的。

现在我们有了这个表格，我们终于可以编写使用它的代码了。这就是我们的普拉特解析器发挥作用的地方。最容易定义的函数是 `getRule()`。

static ParseRule* getRule(TokenType type) {
  return &rules[type];
}

它只是简单地返回给定索引处的规则。它被 `binary()` 调用，用于查找当前运算符的优先级。该函数的存在仅仅是为了处理 C 代码中的一个声明循环。`binary()` 的定义在规则表格之前，这样表格就可以存储指向它的指针。这意味着 `binary()` 的主体不能直接访问表格。

相反，我们将查找封装在一个函数中。这让我们可以在 `binary()` 定义之前前置声明 `getRule()`，并然后在表格之后定义 `getRule()`。我们需要几个其他前置声明来处理语法递归的事实，所以让我们把它们都去掉。

  emitReturn();
}

static void expression();
static ParseRule* getRule(TokenType type);
static void parsePrecedence(Precedence precedence);

static void binary() {

如果你在跟着做，并且自己实现 clox，请密切注意告诉你在哪里放置这些代码片段的小注释。不过，如果你弄错了，C 编译器会很乐意告诉你。

17 . 6 . 1优先级解析

现在我们开始进入有趣的部分。协调我们定义的所有解析函数的指挥家是 `parsePrecedence()`。让我们从解析前缀表达式开始。

static void parsePrecedence(Precedence precedence) {

  advance();
  ParseFn prefixRule = getRule(parser.previous.type)->prefix;
  if (prefixRule == NULL) {
    error("Expect expression.");
    return;
  }

  prefixRule();

}

我们读取下一个标记，并查找相应的 ParseRule。如果没有前缀解析器，那么该标记一定是一个语法错误。我们会报告它并返回给调用者。

否则，我们将调用该前缀解析函数，并让它执行它的任务。该前缀解析器会编译前缀表达式的其余部分，消耗它需要的其他标记，并返回到这里。中缀表达式才是真正有趣的地方，因为优先级在这里发挥作用。其实现非常简单。

  prefixRule();

  while (precedence <= getRule(parser.current.type)->precedence) {
    advance();
    ParseFn infixRule = getRule(parser.previous.type)->infix;
    infixRule();
  }

}

这就是全部。真的。以下是整个函数的工作原理：在 `parsePrecedence()` 的开头，我们查找当前标记的前缀解析器。第一个标记总是会属于某种前缀表达式，这是定义。它可能会被嵌套为一个或多个中缀表达式的操作数，但当你从左到右阅读代码时，你遇到的第一个标记总是属于一个前缀表达式。

解析完它之后（可能会消耗更多标记），前缀表达式就完成了。现在我们查找下一个标记的中缀解析器。如果我们找到了，这意味着我们已经编译的前缀表达式可能是它的操作数。但只有当对 `parsePrecedence()` 的调用具有允许该中缀运算符的足够低的 `precedence` 时，才有可能。

如果下一个标记的优先级过低，或者根本不是中缀运算符，那么我们就完成了。我们已经解析了尽可能多的表达式。否则，我们将消耗该运算符并将控制权移交给我们找到的中缀解析器。它会消耗它需要的其他标记（通常是右操作数），然后返回到 `parsePrecedence()`。然后我们循环回到原点，看看下一个标记是否也是一个有效的可以将整个前缀表达式作为操作数的中缀运算符。我们像这样不断循环，处理中缀运算符及其操作数，直到遇到一个不是中缀运算符或者优先级过低的标记，然后停止。

这段文字讲了很多东西，但是如果你真的想要与沃恩·普拉特心心相印，并完全理解该算法，那么在你的调试器中逐步执行解析器，让它处理一些表达式。也许一张图片可以帮助你。只有几个函数，但它们之间巧妙地相互交织

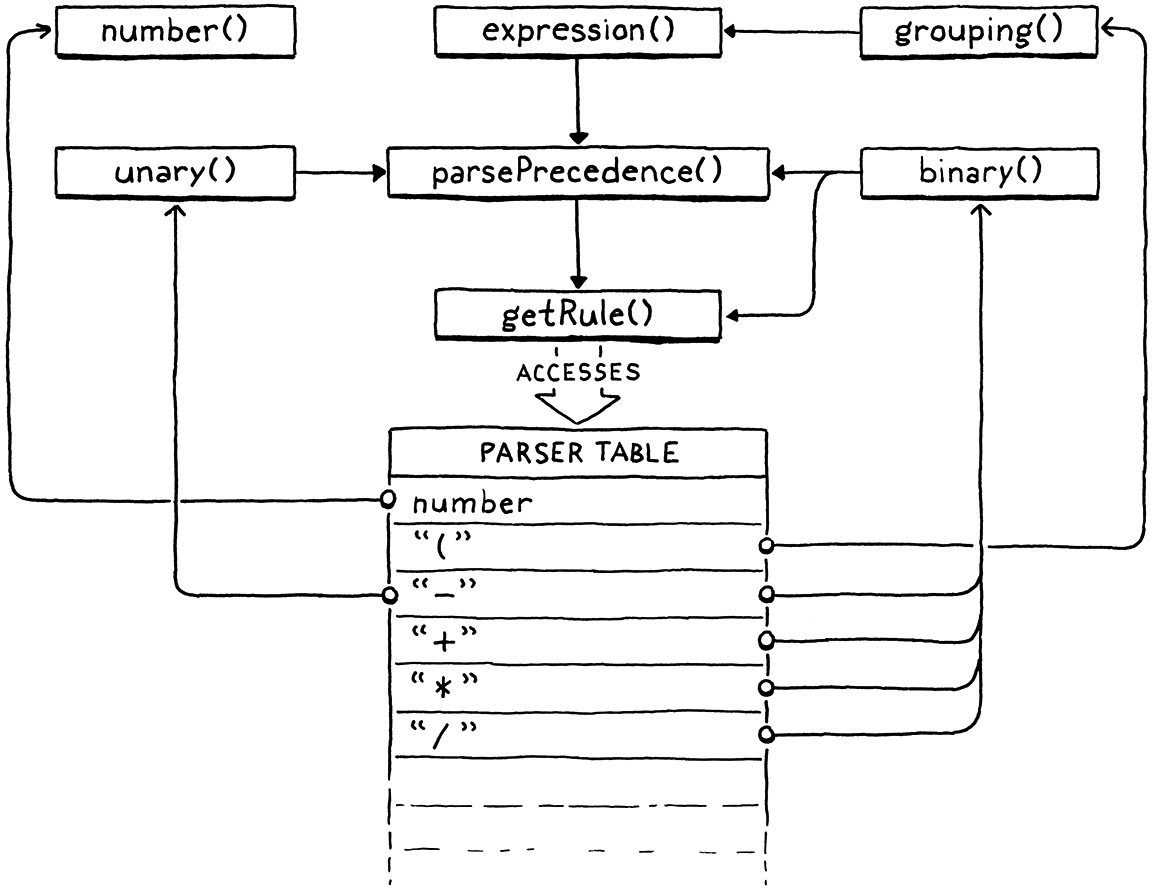
稍后，我们需要调整本章中的代码来处理赋值。但除此之外，我们编写的代码涵盖了本书剩余部分所有表达式编译的需要。当我们添加新的表达式类型时，我们会将其他解析函数插入表格，但 `parsePrecedence()` 是完整的。

17 . 7转储块

趁我们在这里，在编译器的核心部分，我们应该添加一些检测机制。为了帮助调试生成的字节码，我们将添加在编译完成后转储块的支持。我们之前在手工编写块时做了一些临时的日志记录。现在我们将添加一些真正的代码，以便我们可以随时启用它。

由于这不是针对最终用户，所以我们用一个标志将其隐藏起来。

#include <stdint.h>

#define DEBUG_PRINT_CODE

#define DEBUG_TRACE_EXECUTION

如果定义了该标志，我们将使用现有的“debug”模块打印出块的字节码。

  emitReturn();

#ifdef DEBUG_PRINT_CODE
  if (!parser.hadError) {
    disassembleChunk(currentChunk(), "code");
  }
#endif

}

我们只在代码没有错误的情况下执行此操作。在语法错误之后，编译器会继续运行，但它处于一种奇怪的状态，可能会生成错误的代码。这无害，因为它不会被执行，但如果我们尝试读取它，只会让我们自己感到困惑。

最后，要访问 `disassembleChunk()`，我们需要包含它的头文件。

#include "scanner.h"

#ifdef DEBUG_PRINT_CODE
#include "debug.h"
#endif

typedef struct {

我们做到了！这是我们在虚拟机编译和执行管道中安装的最后一个主要部分。我们的解释器看起来并不多，但它内部正在扫描、解析、编译成字节码和执行。

启动虚拟机并输入一个表达式。如果我们一切顺利，它应该计算并打印结果。我们现在拥有一个功能过剩的算术计算器。在接下来的章节中，我们将添加许多语言功能，但基础已经到位。