代码表示
对于居住在森林中的人来说,几乎每种树都有自己的声音和特征。托马斯·哈代,绿林下的树
在 上一章 中,我们以字符串的形式获取原始源代码,并将其转换为更高级别的表示形式:一系列标记。我们在 下一章 中将要编写的解析器,将接收这些标记并再次对其进行转换,以得到更丰富、更复杂的表示形式。
在我们能够生成这种表示形式之前,我们需要对其进行定义。这就是本章要讨论的内容。在此过程中,我们将 涵盖一些关于形式文法的理论,感受函数式编程和面向对象编程之间的区别,回顾几个设计模式,并进行一些元编程。
在我们做完所有这些之前,让我们先关注主要目标—代码的表示。它应该易于解析器生成,也易于解释器使用。如果你还没有编写过解析器或解释器,这些要求并不一定能让你明白。也许你的直觉可以帮助你。当你扮演一个人类解释器的角色时,你的大脑在做什么?你如何在大脑中评估像这样的算术表达式
1 + 2 * 3 - 4
因为你理解运算顺序—古老的“请原谅我亲爱的莎莉阿姨”规则—你知道乘法运算在加法或减法之前进行评估。一种可视化这种优先级的办法是使用树。叶节点是数字,内部节点是运算符,带有表示其每个操作数的分支。
为了评估一个算术节点,你需要知道其子树的数值,因此你必须首先评估它们。这意味着从叶节点向上遍历到根节点—一个后序遍历
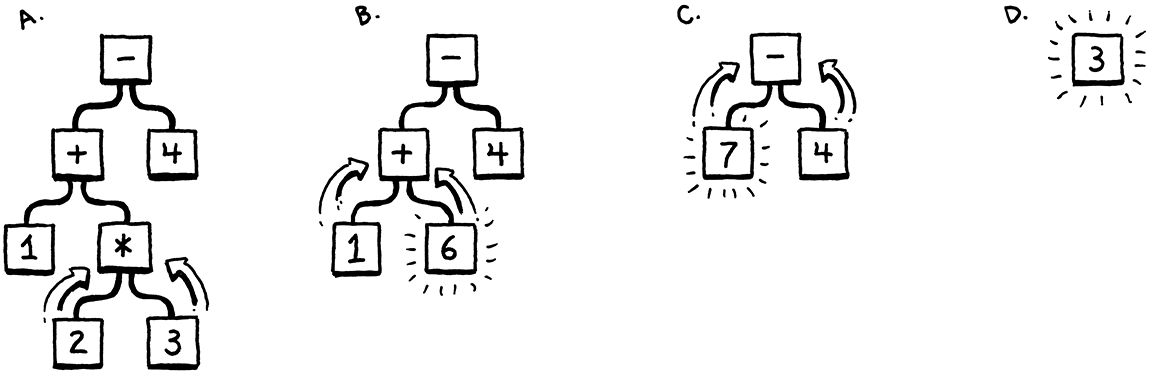
如果我给你一个算术表达式,你可以很容易地画出其中一棵树。给定一棵树,你就可以毫不费力地评估它。因此,直觉上似乎一个可行的代码表示形式是与语法结构—运算符嵌套—相匹配的树。
我们需要更精确地描述这个语法。就像上一章中的词法语法一样,围绕语法语法也存在大量的理论。我们将比扫描时更深入地研究这种理论,因为事实证明它在解释器的许多部分都是一个有用的工具。我们首先向上移动一级乔姆斯基层次结构 . . .
5 . 1上下文无关文法
在上一章中,我们用来定义词法语法—字符如何分组为标记的规则—的形式化被称为正则语言。对于我们的扫描器来说,这是可以的,它会输出一个平坦的标记序列。但正则语言的表达能力不足以处理可以任意嵌套的表达式。
我们需要一个更大的锤子,这个锤子就是上下文无关文法(CFG)。它是形式文法工具箱中下一件最重的工具。形式文法接收一组称为“字母表”的原子组件。然后它定义一个(通常是无限的)“字符串”集合,这些字符串“属于”该文法。每个字符串都是字母表中“字母”的序列。
我使用所有这些引号,因为随着你从词法文法过渡到语法文法,这些术语会变得有点混乱。在我们扫描器的文法中,字母表包含单个字符,字符串是有效的词素—大约相当于“单词”。在现在讨论的语法文法中,我们处于不同的粒度级别。现在字母表中的每个“字母”都是一个完整的标记,一个“字符串”是标记的序列—整个表达式。
哎呀。也许表格会有所帮助
| 术语 | 词法文法 | 语法文法 | |
| “字母表”是 . . . | → | 字符 | 标记 |
| 一个“字符串”是 . . . | → | 词素或标记 | 表达式 |
| 它由 . . .实现 | → | 扫描器 | 解析器 |
形式文法的任务是指定哪些字符串是有效的,哪些不是。如果我们定义一个用于英语句子的文法,那么“鸡蛋是美味的早餐”将在该文法中,但“美味的早餐是鸡蛋”可能不会。
5 . 1 . 1文法的规则
我们如何写下一个包含无限个有效字符串的文法?显然,我们不能将它们全部列出来。相反,我们创建一组有限的规则。你可以将它们视为一个可以“玩”的游戏,并且可以从两个方向“玩”。
如果你从规则开始,你可以用它们来生成属于该文法的字符串。以这种方式创建的字符串称为推导,因为每个字符串都是从文法的规则推导出来的。在游戏的每一步中,你选择一个规则并按照它的指示进行操作。围绕形式文法的术语大部分来自从这个方向玩游戏。规则被称为产生式,因为它们会生成文法中的字符串。
上下文无关文法中的每个产生式都有一个头部—它的名称—和一个主体,它描述了该产生式所生成的内容。在它的纯形式中,主体只是一个符号列表。符号有两种美味的风格
-
一个终结符是文法字母表中的一个字母。你可以把它想象成一个字面值。在我们定义的语法文法中,终结符是单个词素—来自扫描器的标记,例如
if或1234。它们被称为“终结符”,因为它们是“终点”,因为它们不会导致游戏中任何进一步的“移动”。你只需生成那个符号。
-
一个非终结符是指向文法中另一个规则的命名引用。它的意思是“玩那个规则并将它生成的内容插入这里”。通过这种方式,文法组合在一起。
还有一个最后的改进:你可能有多个具有相同名称的规则。当你到达一个具有该名称的非终结符时,你可以选择任何一个规则,无论哪一个最适合你。
为了使这一点具体化,我们需要一个方法来写下这些产生式规则。人们一直在尝试将文法清晰化,一直追溯到帕尼尼的阿斯塔达亚伊,它在几千年前就对梵文语法进行了编纂。直到约翰·巴克斯和他的团队需要一种表示法来指定 ALGOL 58,才有了实质性的进展,他们提出了巴克斯-诺尔范式(BNF)。从那以后,几乎所有人都使用某种形式的 BNF,并根据自己的喜好对其进行调整。
我试图提出一些简洁的东西。每条规则都是一个名称,后面跟着一个箭头(→),然后是一个符号序列,最后以分号(;)结束。终结符是带引号的字符串,非终结符是小写单词。
使用它,这里有一个用于早餐菜单的文法
breakfast → protein "with" breakfast "on the side" ; breakfast → protein ; breakfast → bread ; protein → crispiness "crispy" "bacon" ; protein → "sausage" ; protein → cooked "eggs" ; crispiness → "really" ; crispiness → "really" crispiness ; cooked → "scrambled" ; cooked → "poached" ; cooked → "fried" ; bread → "toast" ; bread → "biscuits" ; bread → "English muffin" ;
我们可以用这个文法来生成随机的早餐。让我们玩一轮,看看它是如何运作的。根据古老的惯例,游戏从文法中的第一条规则开始,这里是breakfast。该规则有三个产生式,我们随机选择第一个产生式。我们得到的字符串如下
protein "with" breakfast "on the side"
我们需要扩展第一个非终结符protein,所以我们为它选择一个产生式。让我们选择
protein → cooked "eggs" ;
接下来,我们需要一个cooked的产生式,所以我们选择"poached"。这是一个终结符,所以我们把它添加进去。现在我们的字符串看起来像这样
"poached" "eggs" "with" breakfast "on the side"
下一个非终结符又是breakfast。我们选择的第一个breakfast产生式递归地引用了breakfast规则。文法中的递归是该语言是上下文无关语言而不是正则语言的一个好兆头。特别是,当递归非终结符在两侧都有产生式时,就意味着该语言不是正则语言。
我们可以一遍又一遍地选择breakfast的第一个产生式,从而产生各种早餐,例如“培根配香肠配炒蛋配培根 . . . ”但我们不会这样做。这次我们将选择bread。该规则有三个产生式,每个产生式只包含一个终结符。我们将选择“英式松饼”。
这样一来,字符串中的每个非终结符都已经被扩展,直到最后只包含终结符,我们得到
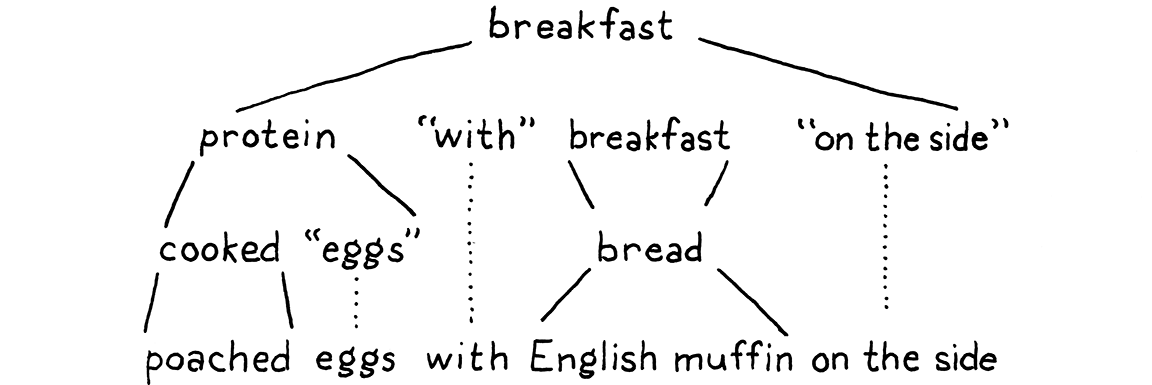
再加上一些火腿和荷兰酱,你就得到了班尼迪克蛋。
无论何时我们遇到一个有多个产生式的规则,我们都只是随机选择一个。正是这种灵活性使少量文法规则能够编码组合起来数量更多的字符串。一个规则可以引用它自身—直接或间接地—这一事实使它变得更加强大,使我们能够将无限多个字符串打包到有限的文法中。
5 . 1 . 2改进我们的符号
将无限多个字符串塞入少数规则中真是太棒了,但我们还可以更进一步。我们的符号表示方法有效,但太繁琐了。所以,像任何优秀的语言设计师一样,我们在上面撒上一些语法糖——一些额外的便捷符号。除了终结符和非终结符,我们还允许在规则体中使用其他几种表达式
-
为了避免每次想要为它添加另一个产生式时都重复规则名称,我们允许使用管道符 (
|) 分隔一系列产生式。bread → "toast" | "biscuits" | "English muffin" ;
-
此外,我们允许使用圆括号进行分组,然后在其中使用
|来从产生式中间的一系列选项中选择一个。protein → ( "scrambled" | "poached" | "fried" ) "eggs" ;
-
使用递归来支持重复的符号序列具有一定的吸引人的 纯度,但每次想要循环时都要创建一个单独命名的子规则,这有点麻烦。所以,我们也使用后缀
*来允许前一个符号或组重复零次或多次。crispiness → "really" "really"* ;
-
后缀
+类似,但要求前面的产生式至少出现一次。crispiness → "really"+ ;
-
后缀
?用于可选的产生式。它前面的东西可以出现零次或一次,但不能更多。breakfast → protein ( "with" breakfast "on the side" )? ;
有了所有这些语法的便利,我们的早餐语法缩减为
breakfast → protein ( "with" breakfast "on the side" )? | bread ; protein → "really"+ "crispy" "bacon" | "sausage" | ( "scrambled" | "poached" | "fried" ) "eggs" ; bread → "toast" | "biscuits" | "English muffin" ;
我希望还不错。如果你习惯了 grep 或者在你的文本编辑器中使用 正则表达式,那么大部分标点符号应该都很熟悉。主要区别在于,这里的符号代表整个标记,而不是单个字符。
我们将在本书的其余部分使用这种符号来精确地描述 Lox 的语法。当你从事编程语言工作时,你会发现上下文无关文法(使用这种符号或 EBNF 或其他一些符号)可以帮助你将你的非正式语法设计理念具体化。它们也是与其他语言黑客交流语法的一种便捷媒介。
我们为 Lox 定义的规则和产生式也是我们对将在内存中表示代码的树形数据结构的指南。在我们能够做到这一点之前,我们需要一个 Lox 的实际语法,或者至少需要我们开始使用的那部分语法。
5 . 1 . 3Lox 表达式的语法
在上一章中,我们一口气完成了 Lox 的整个词法语法。每一个关键字和标点符号都在那里。语法语法更大,如果在我们真正启动解释器之前就遍历整个语法,那将是一件非常枯燥的事情。
相反,我们将在接下来的几章中遍历语言的一个子集。一旦我们有了这个迷你语言的表示、解析和解释,后面的章节就会逐步向其中添加新功能,包括新的语法。现在,我们只关注少数表达式
-
字面量。数字、字符串、布尔值和
nil。 -
一元表达式。前缀
!用于执行逻辑非,-用于对数字取反。 -
二元表达式。我们熟知的、喜欢的中缀算术运算符 (
+,-,*,/) 和逻辑运算符 (==,!=,<,<=,>,>=)。 -
圆括号。一对
(和)包裹在一个表达式周围。
这给了我们足够多的语法来表达像这样的表达式
1 - (2 * 3) < 4 == false
使用我们方便的全新符号,这里是我们对这些表达式的语法
expression → literal | unary | binary | grouping ; literal → NUMBER | STRING | "true" | "false" | "nil" ; grouping → "(" expression ")" ; unary → ( "-" | "!" ) expression ; binary → expression operator expression ; operator → "==" | "!=" | "<" | "<=" | ">" | ">=" | "+" | "-" | "*" | "/" ;
这里有一点额外的 元语法。除了用于匹配精确词素的带引号的字符串之外,我们还将 CAPITALIZE 那些文本表示可能不同的单个词素的终结符。NUMBER 是任何数字字面量,STRING 是任何字符串字面量。稍后,我们将对 IDENTIFIER 做同样的事情。
这个语法实际上是模棱两可的,我们将在解析它时看到这一点。但现在已经足够了。
5 . 2实现语法树
最后,我们开始编写一些代码。这个小小的表达式语法是我们的骨架。由于语法是递归的——注意 grouping、unary 和 binary 如何都引用回 expression——我们的数据结构将形成一棵树。由于这种结构代表了我们语言的语法,所以它被称为 语法树。
我们的扫描器使用了一个单独的 Token 类来表示所有类型的词素。为了区分不同的类型——想想数字 123 与字符串 "123"——我们在其中包含了一个简单的 TokenType 枚举。语法树不像 同构 那样。一元表达式只有一个操作数,二元表达式有两个操作数,字面量没有操作数。
我们可以把所有这些都塞进一个单独的 Expression 类中,这个类包含一个任意的子节点列表。一些编译器就是这样做的。但我喜欢从 Java 的类型系统中获得最大的收益。所以我们将为表达式定义一个基类。然后,对于每种类型的表达式——expression 下面的每个产生式——我们创建一个子类,它包含特定于该规则的非终结符的字段。这样,如果我们试图访问一元表达式的第二个操作数,就会得到编译错误。
就像这样
package com.craftinginterpreters.lox; abstract class Expr { static class Binary extends Expr { Binary(Expr left, Token operator, Expr right) { this.left = left; this.operator = operator; this.right = right; } final Expr left; final Token operator; final Expr right; } // Other expressions... }
Expr 是所有表达式类继承的基类。如你从 Binary 中看到的那样,子类嵌套在其中。这样做没有技术上的必要,但它允许我们将所有类塞进一个单独的 Java 文件中。
5 . 2 . 1迷茫的对象
你会注意到,就像 Token 类一样,这里没有任何方法。这是一个哑结构。类型很好,但仅仅是一个数据包。这在像 Java 这样的面向对象语言中感觉很奇怪。类不应该做些事情吗?
问题在于,这些树类不属于任何一个单独的域。它们应该有解析方法吗,因为解析是创建树的地方?或者解释方法吗,因为解释是使用树的地方?树跨越了这两个区域的边界,这意味着它们实际上既不属于这两个区域。
事实上,这些类型的存在是为了使解析器和解释器能够通信。这使得它们成为只包含数据而不包含任何关联行为的类型。这种风格在像 Lisp 和 ML 这样的函数式语言中非常自然,因为所有数据都与行为分离,但在 Java 中感觉很奇怪。
现在,函数式编程爱好者正在跳起来喊:“看!面向对象语言不适合解释器!” 我不会走那么远。你会记得,扫描器本身非常适合面向对象编程。它拥有所有用于跟踪它在源代码中位置的易变状态,以及一套定义良好的公共方法和少数私有辅助函数。
我的感觉是,解释器的每个阶段或部分在面向对象风格中都能很好地工作。在它们之间流动的正是那些剥夺了行为的数据结构。
5 . 2 . 2元编程树
Java 可以表达无行为类,但我不会说它在这一点上特别出色。用 11 行代码将三个字段塞进一个对象中非常繁琐,而且当我们完成时,我们将拥有 21 个这样的类。
我不想浪费你的时间和我的墨水来写下所有这些。说真的,每个子类的本质是什么?一个名称,以及一个类型化字段列表。仅此而已。我们是很聪明的语言黑客,对吧?让我们 自动化。
与其繁琐地手写每个类的定义、字段声明、构造函数和初始化程序,我们不如编写一个 脚本 来为我们完成这些工作。它包含每个树类型的描述——它的名称和字段——并输出定义具有该名称和状态的类的 Java 代码。
这个脚本是一个小的 Java 命令行应用程序,它生成一个名为“Expr.java”的文件
创建新文件
package com.craftinginterpreters.tool; import java.io.IOException; import java.io.PrintWriter; import java.util.Arrays; import java.util.List; public class GenerateAst { public static void main(String[] args) throws IOException { if (args.length != 1) { System.err.println("Usage: generate_ast <output directory>"); System.exit(64); } String outputDir = args[0]; } }
请注意,此文件位于不同的包中,.tool 而不是 .lox。这个脚本不是解释器本身的一部分。它是我们,那些在解释器上工作的黑客,自己运行的工具,用于生成语法树类。完成后,我们将像对待实现中的任何其他文件一样对待“Expr.java”。我们只是在自动化该文件是如何被编写出来的。
为了生成类,它需要包含对每种类型及其字段的描述。
String outputDir = args[0];
在main()中
defineAst(outputDir, "Expr", Arrays.asList( "Binary : Expr left, Token operator, Expr right", "Grouping : Expr expression", "Literal : Object value", "Unary : Token operator, Expr right" ));
}
为了简洁起见,我把表达式类型的描述塞进了字符串中。每一个都是类的名称,后面跟着 : 和字段列表,用逗号分隔。每个字段都有一个类型和一个名称。
defineAst() 需要做的第一件事是输出基类 Expr。
在main()之后添加
private static void defineAst( String outputDir, String baseName, List<String> types) throws IOException { String path = outputDir + "/" + baseName + ".java"; PrintWriter writer = new PrintWriter(path, "UTF-8"); writer.println("package com.craftinginterpreters.lox;"); writer.println(); writer.println("import java.util.List;"); writer.println(); writer.println("abstract class " + baseName + " {"); writer.println("}"); writer.close(); }
当我们调用它时,baseName 是 “Expr”,它既是类的名称,也是它输出的文件的名称。我们将其作为参数传递,而不是硬编码名称,因为我们稍后将添加一个单独的类族来处理语句。
在基类中,我们定义每个子类。
writer.println("abstract class " + baseName + " {");
在defineAst()中
// The AST classes. for (String type : types) { String className = type.split(":")[0].trim(); String fields = type.split(":")[1].trim(); defineType(writer, baseName, className, fields); }
writer.println("}");
这段代码又调用了
在defineAst()之后添加
private static void defineType( PrintWriter writer, String baseName, String className, String fieldList) { writer.println(" static class " + className + " extends " + baseName + " {"); // Constructor. writer.println(" " + className + "(" + fieldList + ") {"); // Store parameters in fields. String[] fields = fieldList.split(", "); for (String field : fields) { String name = field.split(" ")[1]; writer.println(" this." + name + " = " + name + ";"); } writer.println(" }"); // Fields. writer.println(); for (String field : fields) { writer.println(" final " + field + ";"); } writer.println(" }"); }
好了。所有这些荣耀的 Java 模板都完成了。它声明了类主体中的每个字段。它定义了一个带有每个字段参数的类构造函数,并在主体中初始化它们。
现在编译并运行这个 Java 程序,它会 喷出 一个新的 “.java” 文件,其中包含几十行代码。这个文件马上就要变得更长了。
5 . 3使用树
想象一下。即使我们还没有做到这一点,也要考虑解释器将如何处理语法树。Lox 中的每种表达式在运行时都有不同的行为。这意味着解释器需要选择不同的代码块来处理每种表达式类型。对于标记,我们可以简单地根据 TokenType 进行切换。但我们没有语法树的“类型”枚举,只有一组单独的 Java 类来表示每种类型。
我们可以写一系列类型测试。
if (expr instanceof Expr.Binary) { // ... } else if (expr instanceof Expr.Grouping) { // ... } else // ...
但所有这些顺序类型测试都很慢。名称按字母顺序排在后面的表达式类型执行起来会更慢,因为它们会经过更多 if 语句,才能找到正确的类型。这不是我认为的优雅解决方案。
我们有一组类,需要为每个类关联一部分行为。在像 Java 这样的面向对象语言中,自然而然的解决方案是将这些行为放入类本身的方法中。我们可以在 Expr 上添加一个抽象的 interpret() 方法,然后每个子类都实现它来解释自己。
这对小型项目来说还算可以,但扩展性很差。就像我之前提到的,这些树类跨越了几个领域。至少,解析器和解释器都会对它们进行操作。正如 稍后您将看到的那样,我们需要对它们进行名称解析。如果我们的语言是静态类型的,我们会有一个类型检查过程。
如果我们为表达式类中的每一个操作添加实例方法,那就会将许多不同的领域混杂在一起。这违反了 关注点分离 原则,并会导致难以维护的代码。
5 . 3 . 1表达式问题
这个问题比乍看起来更基本。我们有少量类型和少量高级操作,比如“解释”。对于每对类型和操作,我们都需要一个特定的实现。想象一个表格
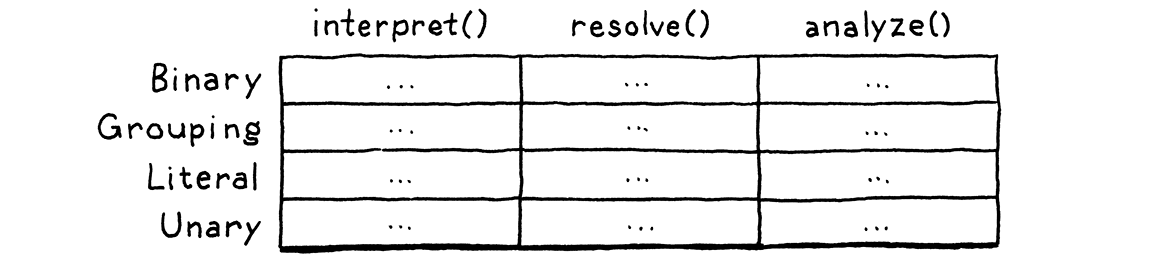
行代表类型,列代表操作。每个单元格代表在该类型上实现该操作的唯一代码片段。
像 Java 这样的面向对象语言假设同一行中的所有代码都自然地联系在一起。它认为对一种类型执行的所有操作都可能相互关联,并且该语言简化了将这些操作定义为同一类中的方法。
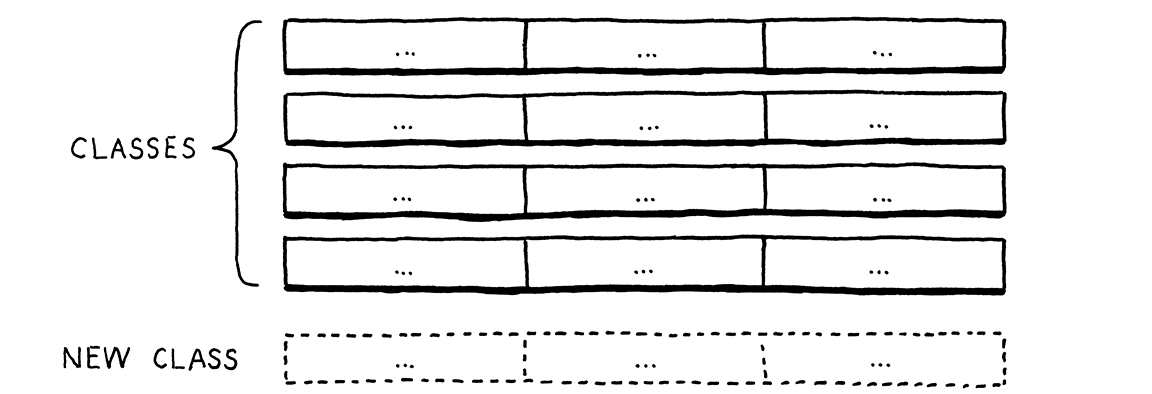
这使得通过添加新行来扩展表格变得容易。只需定义一个新类即可。无需修改任何现有代码。但想象一下,如果您想添加一个新的操作—一列。在 Java 中,这意味着要打开每个现有类并向其中添加一个方法。
在 ML 家族中的函数式编程语言颠覆了这一点。在函数式编程语言中,没有带方法的类。类型和函数是完全独立的。要为多种类型实现一个操作,您需要定义一个单一的函数。在该函数的函数体中,您可以使用模式匹配—一种类似于基于类型的增强版 switch 语句—在同一个位置为每个类型实现操作。
这使得添加新操作变得轻而易举—只需定义另一个对所有类型进行模式匹配的函数。
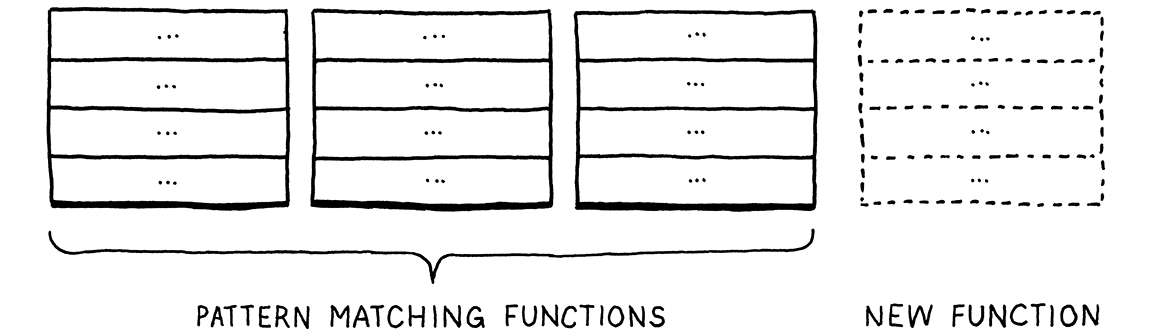
但反过来,添加新的类型就比较困难。您需要返回并向所有现有函数中的所有模式匹配添加新的情况。
每种风格都具有一定的“粒度”。这就是范式名称的字面意思—面向对象语言希望您沿着类型的行组织您的代码。而函数式编程语言则鼓励您将每列的代码组合成一个函数。
许多聪明的语言专家注意到,无论是哪种风格,都无法轻松地向 表格中添加行和列。他们将这种困难称为“表达式问题”,因为—就像我们现在一样—他们在尝试找到在编译器中模拟表达式语法树节点的最佳方式时首先遇到了这个问题。
人们尝试过各种语言特性、设计模式和编程技巧来解决这个问题,但还没有哪种完美的语言能够完全解决它。在目前情况下,我们能做的最好的事就是尝试选择一种语言,其方向与我们正在编写的程序中的自然架构缝合点相匹配。
面向对象编程适用于我们解释器中的许多部分,但这些树类与 Java 的方向不一致。幸运的是,我们可以运用一种设计模式来解决这个问题。
5 . 3 . 2访问者模式
访问者模式是《设计模式》中被误解最深的模式,这在您回顾过去几十年软件架构的过度使用时确实令人惊叹。
问题始于术语。该模式与“访问”无关,其中的“accept”方法也无法唤起任何有用的意象。许多人认为该模式与遍历树有关,但事实并非如此。我们确实将它应用于一组树状类,但这只是一个巧合。正如您将看到的,该模式在单个对象上也能正常工作。
访问者模式实际上是关于在 OOP 语言中模拟函数式风格。它允许我们轻松地向表格中添加新列。我们可以在一个位置为一组类型定义新操作的所有行为,而无需修改类型本身。它通过与我们在计算机科学中解决几乎所有问题相同的方式实现这一点:添加一层间接性。
在我们将其应用于自动生成的 Expr 类之前,让我们先来看一个更简单的例子。假设我们有两种糕点:贝尼特 和甜甜圈。
abstract class Pastry { } class Beignet extends Pastry { } class Cruller extends Pastry { }
我们希望能够定义新的糕点操作—烘焙、食用、装饰等—而无需每次都向每个类添加新方法。以下是如何实现。首先,我们定义一个单独的接口。
interface PastryVisitor { void visitBeignet(Beignet beignet); void visitCruller(Cruller cruller); }
每个可以对糕点执行的操作都是一个新的类,它实现了该接口。它对每种糕点类型都有一个具体方法。这将操作的代码都保存在同一个类中,紧密地放在一起。
给定某个糕点,我们如何根据其类型将其路由到访问者上的正确方法?多态性来救援!我们在糕点类中添加了此方法。
abstract class Pastry {
abstract void accept(PastryVisitor visitor);
}
每个子类都实现它。
class Beignet extends Pastry {
@Override void accept(PastryVisitor visitor) { visitor.visitBeignet(this); }
}
以及
class Cruller extends Pastry {
@Override void accept(PastryVisitor visitor) { visitor.visitCruller(this); }
}
要对糕点执行操作,我们调用它的 accept() 方法,并将我们要执行的操作的访问者传递给它。糕点—具体子类对 accept() 的重写实现—反过来调用访问者上的相应 visit 方法,并将自身传递给它。
这就是技巧的核心所在。它允许我们对糕点类使用多态性分派,以选择访问者类上的相应方法。在表格中,每个糕点类都是一行,但如果您查看单个访问者所有方法,它们会形成一列。
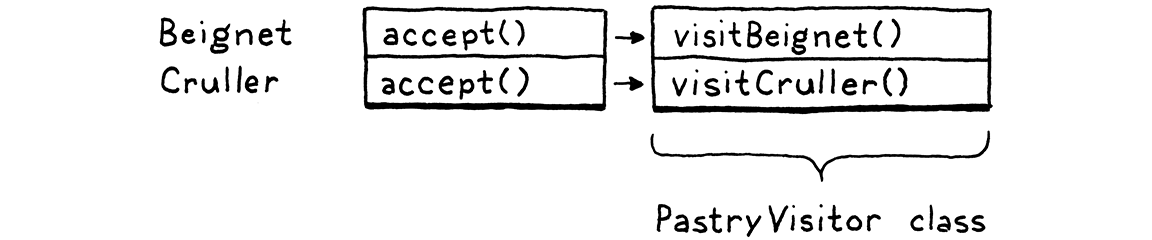
我们在每个类中添加了一个 accept() 方法,并且我们可以使用它来调用任意多个访问者,而无需再次修改糕点类。这是一个巧妙的模式。
5 . 3 . 3表达式的访问者
好的,让我们将其融入我们的表达式类中。我们还将对模式进行一些改进。在糕点示例中,visit 和 accept() 方法不返回任何内容。在实践中,访问者通常希望定义生成值的运算。但 accept() 应该具有什么返回类型?我们无法假设每个访问者类都希望生成相同的类型,因此我们将使用泛型,让每个实现都填写返回类型。
首先,我们定义访问者接口。同样,我们将其嵌套在基类中,以便将所有内容都保存在一个文件中。
writer.println("abstract class " + baseName + " {");
在defineAst()中
defineVisitor(writer, baseName, types);
// The AST classes.
该函数生成访问者接口。
在defineAst()之后添加
private static void defineVisitor( PrintWriter writer, String baseName, List<String> types) { writer.println(" interface Visitor<R> {"); for (String type : types) { String typeName = type.split(":")[0].trim(); writer.println(" R visit" + typeName + baseName + "(" + typeName + " " + baseName.toLowerCase() + ");"); } writer.println(" }"); }
在这里,我们遍历所有子类并为每个子类声明一个 visit 方法。当我们稍后定义新的表达式类型时,这将自动将它们包括在内。
在基类中,我们定义了抽象的 accept() 方法。
defineType(writer, baseName, className, fields);
}
在defineAst()中
// The base accept() method.
writer.println();
writer.println(" abstract <R> R accept(Visitor<R> visitor);");
writer.println("}");
最后,每个子类都实现该方法并调用其自身类型对应的正确 visit 方法。
writer.println(" }");
在 defineType() 中
// Visitor pattern.
writer.println();
writer.println(" @Override");
writer.println(" <R> R accept(Visitor<R> visitor) {");
writer.println(" return visitor.visit" +
className + baseName + "(this);");
writer.println(" }");
// Fields.
就是这样。现在,我们可以定义表达式操作,而无需修改类或生成器脚本。编译并运行此生成器脚本以输出更新的“Expr.java”文件。它包含一个生成的访问者接口和一组支持使用该接口的访问者模式的表达式节点类。
在我们结束本章漫长的旅程之前,让我们实现该访问者接口并观察该模式的实际效果。
5 . 4一个(不太)漂亮的打印机
当我们调试解析器和解释器时,查看解析后的语法树并确保它具有预期的结构通常很有用。我们可以在调试器中检查它,但这可能很麻烦。
相反,我们希望有一些代码,它在给定语法树的情况下,能够生成其无歧义的字符串表示。将树转换为字符串有点类似于解析器的反向操作,通常称为“漂亮打印”,因为其目标是生成一个字符串,该字符串在源语言中是有效的语法。
这并不是我们的目标。我们希望字符串能够非常明确地显示树的嵌套结构。如果我们试图调试的是运算符优先级是否被正确处理,那么返回 1 + 2 * 3 的打印机就没什么帮助了。我们想知道 + 还是 * 在树的顶端。
为此,我们生成的字符串表示不会是 Lox 语法。相反,它看起来很像 Lisp。每个表达式都被显式地括起来,并且所有子表达式和标记都包含在其中。
给定一个类似的语法树
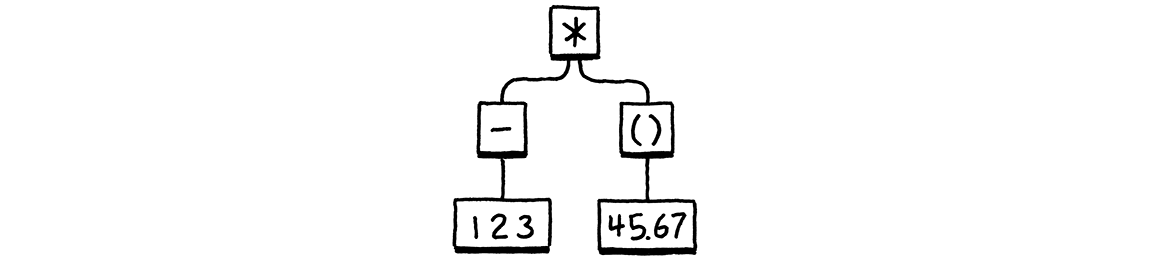
它会生成
(* (- 123) (group 45.67))
不完全是“漂亮”,但它确实明确地显示了嵌套和分组。为了实现这一点,我们定义一个新类。
创建新文件
package com.craftinginterpreters.lox; class AstPrinter implements Expr.Visitor<String> { String print(Expr expr) { return expr.accept(this); } }
如你所见,它实现了访问者接口。这意味着我们需要为到目前为止的每种表达式类型提供访问方法。
return expr.accept(this); }
在 print() 之后添加
@Override public String visitBinaryExpr(Expr.Binary expr) { return parenthesize(expr.operator.lexeme, expr.left, expr.right); } @Override public String visitGroupingExpr(Expr.Grouping expr) { return parenthesize("group", expr.expression); } @Override public String visitLiteralExpr(Expr.Literal expr) { if (expr.value == null) return "nil"; return expr.value.toString(); } @Override public String visitUnaryExpr(Expr.Unary expr) { return parenthesize(expr.operator.lexeme, expr.right); }
}
字面量表达式很简单—它们将值转换为字符串,并进行一些检查以处理 Java 的 null 代表 Lox 的 nil。其他表达式有子表达式,因此它们使用这个 parenthesize() 辅助方法
在 visitUnaryExpr() 之后添加
private String parenthesize(String name, Expr... exprs) { StringBuilder builder = new StringBuilder(); builder.append("(").append(name); for (Expr expr : exprs) { builder.append(" "); builder.append(expr.accept(this)); } builder.append(")"); return builder.toString(); }
它接受一个名称和一个子表达式列表,并将它们全部括起来,生成一个类似于以下的字符串:
(+ 1 2)
请注意,它对每个子表达式调用 accept() 并传入自身。这是使我们能够打印整个树的 递归 步骤。
我们还没有解析器,所以很难看到它在行动。现在,我们将一起拼凑一个小的 main() 方法,它手动实例化一个树并打印它。
在 parenthesize() 之后添加
public static void main(String[] args) { Expr expression = new Expr.Binary( new Expr.Unary( new Token(TokenType.MINUS, "-", null, 1), new Expr.Literal(123)), new Token(TokenType.STAR, "*", null, 1), new Expr.Grouping( new Expr.Literal(45.67))); System.out.println(new AstPrinter().print(expression)); }
如果我们一切都做对了,它会打印
(* (- 123) (group 45.67))
你可以继续删除这个方法。我们不需要它。此外,当我们添加新的语法树类型时,我不会费心展示 AstPrinter 中所需的访问方法。如果你想这样做(并且想要 Java 编译器不要对你大喊大叫),请自己添加它们。在下一章,当我们开始将 Lox 代码解析为语法树时,它会派上用场。或者,如果你不关心维护 AstPrinter,可以随意删除它。我们以后不再需要它。
挑战
-
之前,我说我们添加到语法元语法中的
|、*和+形式只是语法糖。采用以下语法expr → expr ( "(" ( expr ( "," expr )* )? ")" | "." IDENTIFIER )+ | IDENTIFIER | NUMBER
生成一个匹配相同语言但没有使用任何语法糖的语法。
奖励:这段语法编码了什么类型的表达式?
-
访问者模式允许你在面向对象的语言中模拟函数式风格。为函数式语言设计一个互补模式。它应该允许你将所有对一种类型的操作捆绑在一起,并让你轻松地定义新的类型。
(SML 或 Haskell 是这个练习的理想选择,但 Scheme 或其他 Lisp 也可以。)
-
在 逆波兰表示法 (RPN) 中,算术运算符的操作数都放在运算符之前,所以
1 + 2变成了1 2 +。评估从左到右进行。数字被推入隐式栈中。算术运算符弹出前两个数字,执行操作,并将结果压入栈中。因此,这个(1 + 2) * (4 - 3)
在 RPN 中变为
1 2 + 4 3 - *
为我们的语法树类定义一个访问者类,它接受一个表达式,将其转换为 RPN,并返回生成的字符串。