解析表达式
语法,它懂得如何控制即使是国王。 莫里哀
本章标志着本书的第一个重要里程碑。我们中的许多人已经拼凑了一些正则表达式和子字符串操作,试图从一堆文本中提取一些意义。代码可能充满了 bug,并且难以维护。编写一个真正的解析器—一个具有良好的错误处理,一致的内部结构,并且能够稳健地处理复杂的语法—被认为是一项罕见且令人印象深刻的技能。在本章中,你将获得它。
这比你想象的要容易,部分原因是我们前面在上一章中做了很多艰苦的工作。你已经熟悉了形式语法。你熟悉语法树,我们也有一些 Java 类来表示它们。唯一剩下的部分是解析—将一系列标记转换为其中一棵语法树。
一些 CS 教科书对解析器大肆吹嘘。在 60 年代,计算机科学家—很明显厌倦了使用汇编语言编程—开始设计更复杂、更人性化的语言,比如 Fortran 和 ALGOL。不幸的是,对于那个时代的原始计算机来说,它们并不那么机器友好。
这些先驱们设计了他们甚至不确定如何编写编译器的语言,然后做了开创性的工作,发明了可以处理这些新的大型语言和那些老旧的小型机器的解析和编译技术。
经典的编译器书籍读起来就像是对这些英雄和他们的工具的谄媚的传记。编译器:原理、技术和工具的封面实际上有一条龙,上面写着“编译器设计复杂性”,它被一位骑士杀死,骑士手持一把剑和一把盾牌,上面写着“LALR 解析器生成器”和“语法制导翻译”。他们把事情说得太夸张了。
少许的自豪是应该的,但事实是,你不需要了解大多数这些东西就可以为现代机器编写一个高质量的解析器。一如既往,我鼓励你拓宽你的知识面,并在以后学习它,但本书省略了奖杯陈列室。
6 . 1模糊性和解析游戏
在上一章中,我说你可以像玩游戏一样“玩”上下文无关语法来生成字符串。解析器反过来玩这个游戏。给定一个字符串—一系列标记—我们将这些标记映射到语法中的终结符,以找出哪些规则可能生成了该字符串。
“可能已经”部分很有趣。完全有可能创建一个模糊的语法,其中不同的产生式选择可以导致相同的字符串。当你使用语法来生成字符串时,这并不重要。一旦你有了字符串,谁在乎你是如何得到它的呢?
在解析时,模糊意味着解析器可能误解用户的代码。当我们解析时,我们不仅要确定字符串是否是有效的 Lox 代码,还要跟踪哪些规则与字符串的哪些部分匹配,以便我们知道每个标记属于语言的哪个部分。这是我们在上一章中一起构建的 Lox 表达式语法
expression → literal | unary | binary | grouping ; literal → NUMBER | STRING | "true" | "false" | "nil" ; grouping → "(" expression ")" ; unary → ( "-" | "!" ) expression ; binary → expression operator expression ; operator → "==" | "!=" | "<" | "<=" | ">" | ">=" | "+" | "-" | "*" | "/" ;
这是该语法中有效的字符串

但我们有两种方法可以生成它。一种方法是
- 从
expression开始,选择binary。 - 对于左边的
expression,选择NUMBER,并使用6。 - 对于运算符,选择
"/"。 - 对于右边的
expression,再次选择binary。 - 在嵌套的
binary表达式中,选择3 - 1。
另一种方法是
- 从
expression开始,选择binary。 - 对于左边的
expression,再次选择binary。 - 在嵌套的
binary表达式中,选择6 / 3。 - 回到外部
binary,对于运算符,选择"-"。 - 对于右边的
expression,选择NUMBER,并使用1。
它们产生相同的字符串,但不是相同的语法树
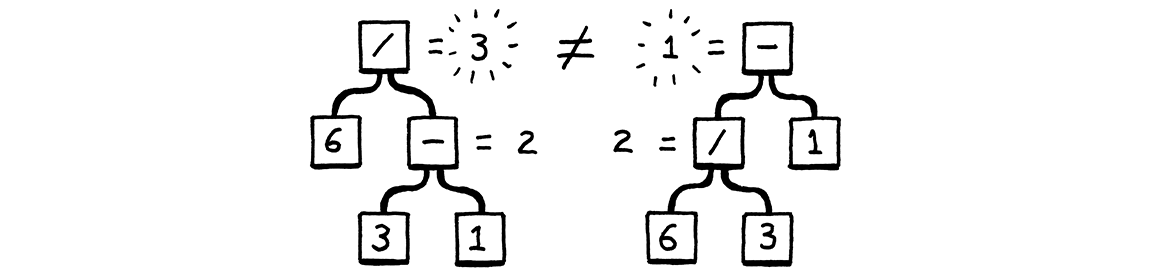
换句话说,语法允许将表达式视为 (6 / 3) - 1 或 6 / (3 - 1)。binary 规则允许操作数以任何你想要的方式嵌套。这反过来会影响解析树的评估结果。自黑板首次出现以来,数学家解决这种模糊性的方法是定义优先级和结合性规则。
-
优先级 决定在包含不同运算符混合的表达式中,哪个运算符首先被评估。优先级规则告诉我们,在上面的例子中,我们先评估
/,然后再评估-。优先级较高的运算符优先于优先级较低的运算符。等效地,优先级较高的运算符被称为“绑定更紧密”。 -
结合性决定在一系列相同运算符中,哪个运算符首先被评估。当运算符是左结合的(想想“从左到右”)时,左边的运算符先于右边的运算符。由于
-是左结合的,所以这个表达式5 - 3 - 1
等同于
(5 - 3) - 1
另一方面,赋值是右结合的。这个
a = b = c
等同于
a = (b = c)
如果没有明确定义的优先级和结合性,使用多个运算符的表达式就是模糊的—它可以解析成不同的语法树,这反过来会导致不同的结果。我们将通过应用与 C 相同的优先级规则来解决 Lox 中的这个问题,从最低到最高。
| 名称 | 运算符 | 结合性 |
| 相等性 | == != |
左 |
| 比较 | > >=
< <= |
左 |
| 项 | - + |
左 |
| 因子 | / * |
左 |
| 一元 | ! - |
右 |
现在,语法将所有表达式类型都塞进了一个 expression 规则中。同一规则用作操作数的非终结符,这允许语法接受任何类型的表达式作为子表达式,无论优先级规则是否允许它。
我们通过分层语法来解决这个问题。我们为每个优先级级别定义一个单独的规则。
expression → ... equality → ... comparison → ... term → ... factor → ... unary → ... primary → ...
这里的每个规则只匹配其优先级级别或更高级别的表达式。例如,unary 匹配一元表达式,比如 !negated,或者主表达式,比如 1234。term 可以匹配 1 + 2,也可以匹配 3 * 4 / 5。最后的 primary 规则涵盖了最高优先级的形式—字面量和括号表达式。
我们只需要填写每个规则的产生式。我们先做简单的。顶级的 expression 规则匹配任何优先级级别的任何表达式。由于equality 具有最低优先级,如果我们匹配它,那么它就涵盖了所有内容。
expression → equality
在优先级表的那一头,主表达式包含所有字面量和分组表达式。
primary → NUMBER | STRING | "true" | "false" | "nil" | "(" expression ")" ;
一元表达式以一元运算符开头,后面跟着操作数。由于一元运算符可以嵌套—!!true 是一个有效的,虽然奇怪的表达式—操作数本身可以是一元运算符。一个递归规则很好地处理了这一点。
unary → ( "!" | "-" ) unary ;
但这个规则有问题。它永远不会终止。
请记住,每个规则都需要匹配该优先级级别或更高级别的表达式,因此我们还需要让它匹配主表达式。
unary → ( "!" | "-" ) unary | primary ;
这可以了。
剩下的规则都是二元运算符。我们先从乘法和除法的规则开始。这是一个初步尝试
factor → factor ( "/" | "*" ) unary | unary ;
该规则递归地匹配左操作数。这使得该规则能够匹配一系列乘法和除法表达式,比如 1 * 2 / 3。将递归产生式放在左侧,将 unary 放在右侧,使规则左结合且无歧义。
所有这些都是正确的,但事实是,规则主体中的第一个符号与规则的头部相同,这意味着这个产生式是左递归的。一些解析技术,包括我们即将使用的技术,难以处理左递归。(其他地方的递归,比如我们已经在 unary 中使用的递归,以及 primary 中用于分组的间接递归,都不是问题。)
您可以定义许多匹配同一种语言的语法。如何对特定语言建模的选择部分取决于个人喜好,部分取决于实际情况。这条规则是正确的,但对于我们想要解析的方式来说不是最佳的。我们将使用不同的规则来代替左递归规则。
factor → unary ( ( "/" | "*" ) unary )* ;
我们将因子表达式定义为乘法和除法的扁平序列。这与之前的规则匹配相同的语法,但更好地反映了我们将编写用于解析 Lox 的代码。我们对所有其他二元运算符优先级级别使用相同的结构,从而得到完整的表达式语法。
expression → equality ; equality → comparison ( ( "!=" | "==" ) comparison )* ; comparison → term ( ( ">" | ">=" | "<" | "<=" ) term )* ; term → factor ( ( "-" | "+" ) factor )* ; factor → unary ( ( "/" | "*" ) unary )* ; unary → ( "!" | "-" ) unary | primary ; primary → NUMBER | STRING | "true" | "false" | "nil" | "(" expression ")" ;
此语法比我们之前使用的语法更复杂,但作为回报,我们消除了之前语法的歧义。这正是我们制作解析器所需的。
6 . 2递归下降解析
有一整套解析技术的名称大多是“L”和“R”的组合—LL(k),LR(1),LALR—以及更奇特的野兽,如 解析器组合器,Earley 解析器,移位-归约算法,和 packrat 解析。对于我们的第一个解释器,一种技术就足够了:递归下降。
递归下降是构建解析器的最简单方法,不需要使用像 Yacc、Bison 或 ANTLR 这样的复杂解析器生成工具。您只需要直接的手写代码。不过,不要被它的简单性所迷惑。递归下降解析器速度快,健壮,并且可以支持复杂的错误处理。事实上,GCC、V8(Chrome 中的 JavaScript VM)、Roslyn(用 C# 编写的 C# 编译器)以及许多其他重量级的生产语言实现都使用递归下降。它很棒。
递归下降被认为是一种自顶向下解析器,因为它从顶层或最外层的语法规则(这里是 expression)开始,然后向下进入嵌套的子表达式,最终到达语法树的叶子节点。这与 LR 这样的自底向上解析器形成对比,自底向上解析器从基本表达式开始,并将它们组合成越来越大的语法块。
递归下降解析器是对语法的规则的直接翻译,直接转换为命令式代码。每个规则都成为一个函数。规则的主体大致转换为类似于以下代码的代码。
| 语法表示法 | 代码表示 |
| 终结符 | 匹配和使用令牌的代码 |
| 非终结符 | 调用该规则的函数 |
| | if 或 switch 语句 |
* 或 + | while 或 for 循环 |
? | if 语句 |
下降被称为“递归”,因为当语法规则引用自身时—直接或间接地—它会转换为递归函数调用。
6 . 2 . 1解析器类
每个语法规则都成为此新类中的一个方法。
创建新文件
package com.craftinginterpreters.lox; import java.util.List; import static com.craftinginterpreters.lox.TokenType.*; class Parser { private final List<Token> tokens; private int current = 0; Parser(List<Token> tokens) { this.tokens = tokens; } }
与扫描器一样,解析器使用扁平的输入序列,只是现在我们读取的是令牌而不是字符。我们存储令牌列表,并使用 current 指向等待解析的下一个令牌。
我们现在将直接运行表达式语法,并将每个规则转换为 Java 代码。第一个规则 expression 只扩展到 equality 规则,因此这很简单。
在 Parser() 之后添加
private Expr expression() { return equality(); }
解析语法规则的每个方法都会为该规则生成语法树,并将其返回给调用者。当规则的主体包含非终结符—对另一条规则的引用—时,我们调用该规则方法。
相等性规则稍微复杂一些。
equality → comparison ( ( "!=" | "==" ) comparison )* ;
在 Java 中,它变成了
在 expression() 之后添加
private Expr equality() { Expr expr = comparison(); while (match(BANG_EQUAL, EQUAL_EQUAL)) { Token operator = previous(); Expr right = comparison(); expr = new Expr.Binary(expr, operator, right); } return expr; }
让我们逐步讲解。主体中的第一个 comparison 非终结符转换为方法中对 comparison() 的第一次调用。我们将结果存储在局部变量中。
然后,规则中的 ( ... )* 循环映射到 while 循环。我们需要知道何时退出该循环。我们可以看到,在规则内部,我们必须首先找到 != 或 == 令牌。因此,如果我们没有看到其中之一,我们必须完成相等运算符的序列。我们使用一个方便的 match() 方法来表示该检查。
在 equality() 之后添加
private boolean match(TokenType... types) { for (TokenType type : types) { if (check(type)) { advance(); return true; } } return false; }
这会检查当前令牌是否具有给定类型。如果是,则使用令牌并返回 true。否则,它将返回 false 并且不使用当前令牌。match() 方法是根据另外两个更基本的操作定义的。
check() 方法如果当前令牌为给定类型,则返回 true。与 match() 不同,它永远不会使用令牌,它只查看令牌。
在 match() 之后添加
private boolean check(TokenType type) { if (isAtEnd()) return false; return peek().type == type; }
advance() 方法使用当前令牌并将其返回,类似于我们的扫描器对应的方法如何遍历字符。
在 check() 之后添加
private Token advance() { if (!isAtEnd()) current++; return previous(); }
这些方法最终归结为最后几个基本操作。
在 advance() 之后添加
private boolean isAtEnd() { return peek().type == EOF; } private Token peek() { return tokens.get(current); } private Token previous() { return tokens.get(current - 1); }
isAtEnd() 检查我们是否已解析完所有令牌。peek() 返回我们尚未使用的当前令牌,previous() 返回最近使用的令牌。后者使使用 match() 然后访问刚刚匹配的令牌变得更容易。
这就是我们需要的解析基础设施的大部分。我们在哪里?对了,所以如果我们在 equality() 中的 while 循环中,那么我们知道我们找到了一个 != 或 == 运算符,并且必须解析一个相等表达式。
我们获取匹配的运算符令牌,以便跟踪我们具有的相等表达式类型。然后,我们再次调用 comparison() 来解析右手操作数。我们将运算符及其两个操作数组合到一个新的 Expr.Binary 语法树节点中,然后循环。对于每次迭代,我们将结果表达式存储回同一个 expr 局部变量中。当我们遍历一系列相等表达式时,这会创建一个左结合的二元运算符节点的嵌套树。
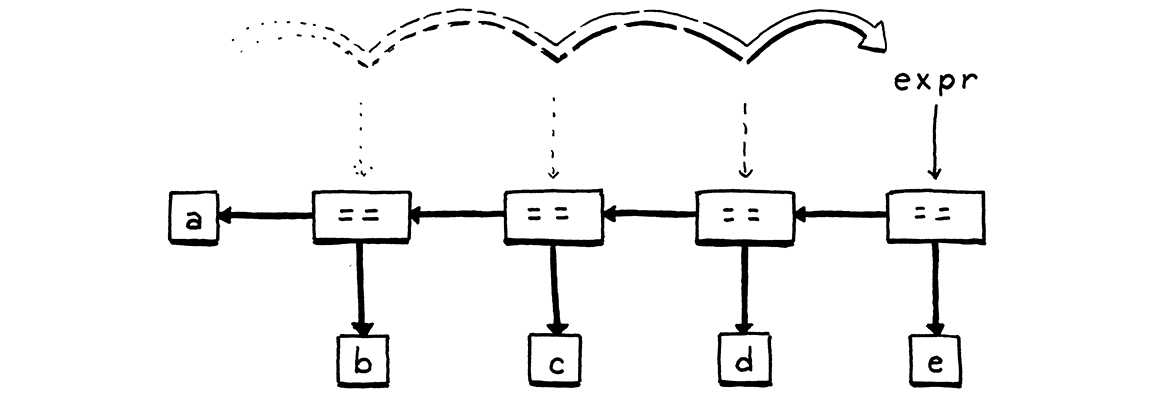
一旦解析器遇到一个不是相等运算符的令牌,它就会退出循环。最后,它返回表达式。请注意,如果解析器从未遇到相等运算符,那么它就不会进入循环。在这种情况下,equality() 方法有效地调用并返回 comparison()。通过这种方式,此方法匹配相等运算符或任何更高优先级的运算符。
继续下一个规则 . . .
comparison → term ( ( ">" | ">=" | "<" | "<=" ) term )* ;
转换为 Java
在 equality() 之后添加
private Expr comparison() { Expr expr = term(); while (match(GREATER, GREATER_EQUAL, LESS, LESS_EQUAL)) { Token operator = previous(); Expr right = term(); expr = new Expr.Binary(expr, operator, right); } return expr; }
语法规则实际上与 equality相同,相应的代码也是如此。唯一的区别是匹配的运算符的令牌类型以及我们为操作数调用的方法—现在是 term() 而不是 comparison()。剩下的两个二元运算符规则遵循相同的模式。
按优先级排序,首先是加法和减法
在 comparison() 之后添加
private Expr term() { Expr expr = factor(); while (match(MINUS, PLUS)) { Token operator = previous(); Expr right = factor(); expr = new Expr.Binary(expr, operator, right); } return expr; }
最后,乘法和除法
在 term() 之后添加
private Expr factor() { Expr expr = unary(); while (match(SLASH, STAR)) { Token operator = previous(); Expr right = unary(); expr = new Expr.Binary(expr, operator, right); } return expr; }
这就是所有二元运算符,以正确的优先级和结合性进行解析。我们正在向上爬优先级层次结构,现在我们已经到达了一元运算符。
unary → ( "!" | "-" ) unary | primary ;
此代码略有不同。
在 factor() 之后添加
private Expr unary() { if (match(BANG, MINUS)) { Token operator = previous(); Expr right = unary(); return new Expr.Unary(operator, right); } return primary(); }
同样,我们查看当前令牌,以了解如何解析。如果它是 ! 或 -,那么我们一定有一个一元表达式。在这种情况下,我们将令牌抓取,然后递归调用 unary() 再次解析操作数。将所有这些都包装在一个一元表达式语法树中,我们就完成了。
否则,我们一定已经到达了最高优先级,即基本表达式。
primary → NUMBER | STRING | "true" | "false" | "nil" | "(" expression ")" ;
规则的大多数情况都是单个终结符,因此解析很简单。
在 unary() 之后添加
private Expr primary() { if (match(FALSE)) return new Expr.Literal(false); if (match(TRUE)) return new Expr.Literal(true); if (match(NIL)) return new Expr.Literal(null); if (match(NUMBER, STRING)) { return new Expr.Literal(previous().literal); } if (match(LEFT_PAREN)) { Expr expr = expression(); consume(RIGHT_PAREN, "Expect ')' after expression."); return new Expr.Grouping(expr); } }
有趣的分支是处理括号的那部分。在匹配了开头的 ( 并解析了其内部的表达式之后,我们必须找到 ) 令牌。如果没有,那就是错误。
6 . 3语法错误
解析器实际上有两个工作
-
给定有效的令牌序列,生成相应的语法树。
-
给定无效的令牌序列,检测任何错误并告诉用户他们的错误。
不要低估第二项工作的重要性!在现代 IDE 和编辑器中,解析器会不断地重新解析代码—通常在用户仍在编辑代码时—以进行语法高亮并支持诸如自动完成之类的事情。这意味着它会一直遇到不完整、错误状态的代码。
当用户没有意识到语法错误时,解析器有责任帮助他们回到正确的道路上。它报告错误的方式是您语言用户界面的一部分。良好的语法错误处理很难。根据定义,代码不是处于定义良好的状态,因此没有万无一失的方法可以知道用户想要写什么。解析器无法读懂您的思想.
当解析器遇到语法错误时,有一些硬性要求。解析器必须
-
检测并报告错误。如果它没有检测到错误并将生成的畸形语法树传递给解释器,那么可能会出现各种恐怖事件。
-
避免崩溃或挂起。语法错误是生活中不可避免的事情,语言工具必须能够应对这些错误。不允许出现段错误或陷入死循环。虽然源代码可能不是有效的代码,但它仍然是解析器的有效输入,因为用户使用解析器来了解允许的语法。
如果你想参与解析器游戏,这些都是必须具备的条件,但你真的想要更上一层楼。一个不错的解析器应该
-
速度快。 计算机的速度比解析器技术首次发明时快了数千倍。在咖啡休息时间内,需要优化解析器以使其能够处理整个源文件的日子已经过去了。但是程序员的期望却在快速增长,甚至更快。他们期望他们的编辑器在每次按键后以毫秒为单位重新解析文件。
-
报告尽可能多的不同错误。 在第一个错误后中止很容易实现,但如果每次用户修复他们认为文件中的一个错误时,都会出现一个新错误,这对用户来说很烦人。他们希望看到所有错误。
-
将级联错误降到最低。 一旦找到一个错误,解析器就无法真正知道发生了什么。它尝试让自身恢复正常并继续执行,但如果它感到困惑,它可能会报告一系列幽灵错误,这些错误并不表示代码中存在其他实际问题。当第一个错误被修复时,这些幽灵就会消失,因为它们只反映了解析器自身的困惑。级联错误很烦人,因为它们会让用户感到害怕,认为他们的代码比实际情况更糟糕。
最后两点存在矛盾。我们希望报告尽可能多的单独错误,但我们不想报告仅仅是先前错误的副作用的错误。
解析器对错误的响应方式以及如何继续查找后续错误被称为错误恢复。这在 60 年代是一个热门的研究课题。那时,你会把一堆穿孔卡片交给秘书,第二天回来看看编译器是否成功。有了如此缓慢的迭代循环,你真的希望在一遍扫描中找到代码中的每一个错误。
如今,当解析器在你完成输入之前就完成时,这已经不是什么大问题了。简单、快速的错误恢复就足够了。
6 . 3 . 1恐慌模式错误恢复
在所有过去发明的恢复技术中,最能经受住时间考验的一种被称为—有点令人担忧—恐慌模式。一旦解析器检测到错误,它就会进入恐慌模式。它知道至少有一个标记在某种语法产生式堆栈中间的当前状态下没有意义。
在它能够恢复解析之前,它需要使其状态和即将出现的标记序列对齐,以便下一个标记与正在解析的规则匹配。这个过程被称为同步。
为了做到这一点,我们选择语法中的某个规则来标记同步点。解析器通过跳出任何嵌套的产生式,直到回到该规则,从而修复其解析状态。然后它通过丢弃标记,直到到达规则中该点可以出现的标记,从而同步标记流。
那些被丢弃的标记中隐藏的任何其他真实语法错误都不会被报告,但这也意味着,任何仅仅是初始错误的副作用的错误的级联错误都不会被错误地报告,这是一个不错的权衡。
语法中传统用于同步的地方是在语句之间。我们还没有这些,所以我们不会在本章中实际同步,但我们会为以后做好准备。
6 . 3 . 2进入恐慌模式
在我们绕道进行错误恢复之前,我们正在编写解析带括号表达式的代码。解析完表达式后,解析器通过调用consume()来查找闭合的)。终于,这就是这个方法
在 match() 之后添加
private Token consume(TokenType type, String message) { if (check(type)) return advance(); throw error(peek(), message); }
它与match()类似,因为它检查下一个标记是否为预期类型。如果是,它会消耗该标记,一切都很好。如果存在其他标记,那么我们遇到错误。我们通过调用以下方法来报告错误
添加在previous()之后
private ParseError error(Token token, String message) { Lox.error(token, message); return new ParseError(); }
首先,它通过调用以下方法向用户显示错误
添加在report()之后
static void error(Token token, String message) { if (token.type == TokenType.EOF) { report(token.line, " at end", message); } else { report(token.line, " at '" + token.lexeme + "'", message); } }
这在给定的标记处报告错误。它显示标记的位置和标记本身。这在以后会很有用,因为我们在整个解释器中使用标记来跟踪代码中的位置。
在报告完错误后,用户知道了自己的错误,但解析器接下来做什么?回到error()中,我们创建并返回 ParseError,这是一个新类的实例
class Parser {
嵌套在类Parser内部
private static class ParseError extends RuntimeException {}
private final List<Token> tokens;
这是一个简单的哨兵类,我们用它来解开解析器。error()方法返回错误而不是抛出错误,因为我们希望让解析器内部的调用方法决定是否解开。一些解析错误发生在解析器不太可能进入奇怪状态的地方,我们不需要同步。在这些地方,我们只需报告错误并继续执行。
例如,Lox 限制了你可以传递给函数的参数数量。如果你传递了太多参数,解析器需要报告该错误,但它可以并且应该继续解析额外的参数,而不是惊慌失措并进入恐慌模式。
然而,在我们的例子中,语法错误很严重,因此我们想要恐慌并同步。丢弃标记非常容易,但是我们如何同步解析器自身的 state?
6 . 3 . 3同步递归下降解析器
使用递归下降,解析器的状态—它处于识别中间的规则—没有在字段中显式存储。相反,我们使用 Java 自身的调用堆栈来跟踪解析器正在做什么。正在解析中间的每个规则都是堆栈上的一个调用帧。为了重置该状态,我们需要清除这些调用帧。
在 Java 中,最自然的方法是使用异常。当我们想要同步时,我们抛出该 ParseError 对象。在我们要同步到的语法规则方法的更高层,我们将捕获它。由于我们在语句边界上同步,因此我们将在那里捕获异常。在捕获异常后,解析器处于正确状态。剩下要做的就是同步标记。
我们希望丢弃标记,直到我们正好位于下一个语句的开头。这个边界很容易识别—这是我们选择它的主要原因之一。在分号之后,我们可能完成了语句。大多数语句都以关键字开头—for、if、return、var 等。当下一个标记是这些关键字中的任何一个时,我们可能即将开始一个语句。
这个方法封装了该逻辑
添加在error()之后
private void synchronize() { advance(); while (!isAtEnd()) { if (previous().type == SEMICOLON) return; switch (peek().type) { case CLASS: case FUN: case VAR: case FOR: case IF: case WHILE: case PRINT: case RETURN: return; } advance(); } }
它丢弃标记,直到它认为已经找到了语句边界。在捕获 ParseError 后,我们将调用它,然后我们有望重新同步。当它正常工作时,我们已经丢弃了可能导致级联错误的标记,现在我们可以从下一个语句开始解析文件的其余部分。
唉,我们还没有看到这个方法的实际作用,因为我们还没有语句。我们会在接下来的几章中谈到它。现在,如果发生错误,我们将恐慌并一直解开到顶部并停止解析。由于我们只能解析单个表达式,所以这没什么损失。
6 . 4连接解析器
我们现在已经完成了对表达式的解析。还有一个地方需要添加一些错误处理。当解析器下降到每个语法规则的解析方法时,它最终会到达primary()。如果那里的任何情况都不匹配,则意味着我们正在一个不能开始表达式的标记上。我们也需要处理这个错误。
if (match(LEFT_PAREN)) {
Expr expr = expression();
consume(RIGHT_PAREN, "Expect ')' after expression.");
return new Expr.Grouping(expr);
}
在primary()中
throw error(peek(), "Expect expression.");
}
这样一来,解析器中剩下的就是定义一个初始方法来启动它。这个方法自然地被称为parse()。
在 Parser() 之后添加
Expr parse() { try { return expression(); } catch (ParseError error) { return null; } }
我们将在以后添加语句到语言中时重新访问这个方法。现在,它解析一个表达式并返回它。我们还有一些临时代码退出恐慌模式。语法错误恢复是解析器的任务,因此我们不希望 ParseError 异常逃逸到解释器的其他部分。
当发生语法错误时,这个方法会返回null。没关系。解析器承诺不会在无效语法上崩溃或挂起,但它不承诺在发现错误时返回可用的语法树。一旦解析器报告错误,hadError就会被设置,后续阶段将被跳过。
最后,我们可以将我们全新的解析器连接到主 Lox 类并尝试一下。我们还没有解释器,所以现在,我们将解析到语法树,然后使用上一章中的 AstPrinter 类来显示它。
删除打印扫描标记的旧代码,并用以下代码替换它
List<Token> tokens = scanner.scanTokens();
在run()中
替换 5 行
Parser parser = new Parser(tokens); Expr expression = parser.parse(); // Stop if there was a syntax error. if (hadError) return; System.out.println(new AstPrinter().print(expression));
}
恭喜你,你已经跨过了门槛!这确实是手工编写解析器的全部内容。我们将在以后的章节中使用赋值、语句和其他内容扩展语法,但这些内容都不比我们在这里处理的二元运算符更复杂。
启动解释器并输入一些表达式。看看它是否正确处理了优先级和结合性?不到 200 行代码就能做到这一点,还不错。
挑战
-
在 C 语言中,块是一种语句形式,它允许你将一系列语句打包到一个期望单个语句的地方。 逗号运算符是表达式的一种类似语法。可以给出逗号分隔的一系列表达式,这些表达式可以用于期望单个表达式的场合(函数调用参数列表除外)。在运行时,逗号运算符会评估左操作数并丢弃结果。然后它会评估右操作数并返回结果。
添加对逗号表达式的支持。赋予它们与 C 中相同的优先级和结合性。编写语法,然后实现必要的解析代码。
-
同样,添加对 C 风格的条件或“三元”运算符
?:的支持。?和:之间的优先级级别允许为多少?整个运算符是左结合还是右结合? -
添加错误产生式以处理每个二元运算符在没有左操作数的情况下出现的情况。换句话说,检测二元运算符出现在表达式的开头。将其报告为错误,但也解析并丢弃具有适当优先级的右操作数。
设计说明:逻辑与历史
假设我们决定在 Lox 中添加按位 & 和 | 运算符。我们应该将它们放在优先级层次结构的哪个位置?C—以及大多数遵循 C 脚步的语言—将它们放在 == 之下。这被广泛认为是一个错误,因为它意味着常见的操作(如测试标志)需要括号。
if (flags & FLAG_MASK == SOME_FLAG) { ... } // Wrong. if ((flags & FLAG_MASK) == SOME_FLAG) { ... } // Right.
我们应该为 Lox 修复此问题,并将按位运算符放在优先级表中高于 C 的位置吗?我们可以采取两种策略。
你几乎永远不想使用 == 表达式的结果作为按位运算符的操作数。通过使按位运算符绑定更紧密,用户不必经常使用括号。因此,如果我们这样做,而用户假设优先级是逻辑选择以最小化括号,他们很可能正确推断出来。
这种内部一致性使语言更易于学习,因为用户需要偶然发现并纠正的边缘情况和异常更少。这很好,因为在用户可以使用我们的语言之前,他们必须将所有语法和语义加载到他们的大脑中。一种更简单、更合理的语言有意义。
但是,对于许多用户来说,有一种更快的捷径可以将我们的语言理念纳入他们的湿件—使用他们已经知道的概念。许多我们的语言的新手将来自其他语言或语言。如果我们的语言使用与这些语言相同的语法或语义,用户需要学习(和遗忘)的东西就会少得多。
这对于语法尤其有用。你今天可能不记得了,但当你学习你的第一门编程语言时,代码可能看起来很陌生且难以接近。只有通过艰苦的努力,你才学会阅读和接受它。如果你为你的新语言设计了一种新颖的语法,你将迫使用户重新开始这个过程。
利用用户已知的东西是你用来简化语言采用的最强大的工具之一。它的价值几乎无法估量。但这会让你面临一个棘手的问题:如果用户都知道的东西有点糟糕怎么办?C 的按位运算符优先级是一个错误,没有意义。但它是一个熟悉的错误,数百万人都已经习惯并学会了接受。
你是否要忠于你语言自身的内部逻辑并忽略历史?你是否要从一张白纸和第一性原理开始?或者你是否要将你的语言融入丰富的编程历史之中,通过从用户已经知道的东西开始来帮助他们入门?
这里没有完美的答案,只有权衡。你和我都明显偏向于喜欢新颖的语言,因此我们自然的倾向是焚烧历史书籍,开始我们自己的故事。
在实践中,充分利用用户已经知道的东西通常更好。让他们来到你的语言需要一个很大的飞跃。你能使这个鸿沟越小,就越多人愿意跨越它。但你不能总是坚持历史,否则你的语言将不会有新的和引人入胜的东西让人们有理由跳跃。